练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，要设计一幅长为60cm，宽为40cm的矩形图案，其中有两横两竖的矩形彩条，横竖彩条宽度比为1：2，若彩条所占面积是图案面积的一半，求一条横彩条的宽度．

    分析 设一条横彩条的宽度为xcm，则一条竖彩条的宽度为2xcm．根据“彩条所占面积是图案面积的一半”列出方程并解答即可．

    解答 解：设一条横彩条的宽度为xcm，则一条竖彩条的宽度为2xcm．
    根据题意得（60-2×2x）（40-2x）=$\frac{1}{2}×60×40$，
    整理得   x2-35x+150=0，
    解得x1=5，x2=35，
    当x=35时，40-2x＜0，不合题意，舍去．
    答：一条横彩条的宽度为5cm．

    点评 本题考查的是一元二次方程的应用，设出横、竖条的宽，以面积做为等量关系列方程求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．如图，AB=AC，AD=AE，CD=BE．求证：∠DAB=∠EAC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知a，b，c在数轴上的位置如图所示，所对应的点分别为A，B，C．
    （1）填空：A、B之间的距离为a-b，B、C之间的距离为b-c，A、C之间的距离为a-c；
    （2）化简：|a+b|-|c-b|+|b-a|；
    （3）a、b、c在数轴上的位置如图所示，且c2=4，-b的倒数是它本身，a的绝对值的相反数是-2，求-a+2b-c-2（a-4c-b）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，点A从原点出发沿数轴向左运动，同时，点B也从原点出发沿数轴向右运动，5秒后，两点相距15个单位长度．已知点B的速度是点A的速度的2倍（速度单位：单位长度/秒）．
    （1）求出点A、点B运动的速度，并在数轴上标出A、B两点从原点出发运动5秒时的位置；

    （2）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动，再过几秒时，原点恰好处在点A、点B的正中间？
    （3）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点C同时从原点O位置出发向B点运动，且C的速度是点A的速度的一半；当C运动几秒后，C为AB的中点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

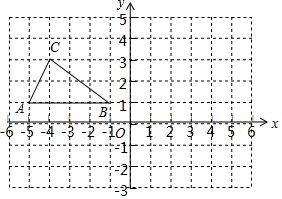    10．如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（-5，1），B（-1，1），C（-4，3）．
    （1）若△A1B1C1与△ABC关于y轴对称，点A，B，C的对应点分别为A1，B1，C1，请画出△A1B1C1并写出A1，B1，C1的坐标；
    （2）若点P为平面内不与C重合的一点，△PAB与△ABC全等，请写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

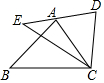    20．如图所示，△ABC≌△DEC，∠ACB=60°，∠BCD=100°，点A恰好落在线段ED上，则∠B的度数为（　　）
    A．50°B．60°C．55°D．65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

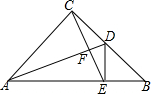    7．如图所示，△ABC是等腰直角三角形，∠ACB=90°，AD是BC边上的中线，过C作AD的垂线，交AB于点E，交AD于点F．
    求证：（1）∠ADC=∠BDE；（用两种方法证明）
    （2）CE+DE=AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在学习代数式的值时，介绍了计算框图：用“”表示数据输入、输出框；用“”表示数据处理和运算框；用“”表示数据判断框（根据条件决定执行两条路径中的某一条）
    （1）①如图1，当输入数x=-2时，输出数y=-9；
    ②如图2，第一个运算框“”内，应填×5；第二个运算框“”内，应填-3；
    （2）①如图3，当输入数x=-1时，输出数y=-43；
    ②如图4，当输出的值y=37，则输入的值x=42或-6；
    （3）为鼓励节约用水，决定对用水实行“阶梯价”：当每月用水量不超过15吨时（含15吨），以2元/吨的价格收费；当每月用水量超过15吨时，超过部分以3元/吨的价格收费．请设计出一个“计算框图”，使得输入数为用水量x，输出数为水费y．

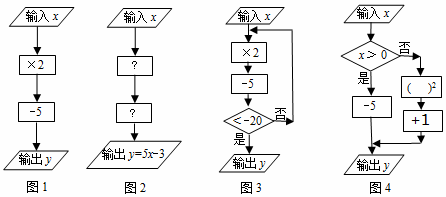
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列各题计算：
    ?①（-24）÷（-8）=3；
    ?②36÷（-9）=4；?
    ③（-3）×4÷$\frac{1}{3}$=-4；   
    ④（-5.25-2.25+6.25）×0=-1  
    其中正确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    同步练习册答案