
【题目】如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
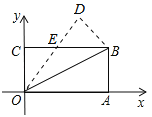
A.(4,8) B.(5,8) C.(![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20. 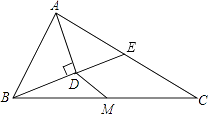
(1)求证:BD=DE;
(2)求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
(1)小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.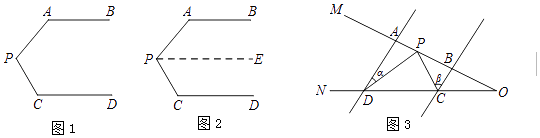
(2)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(3)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
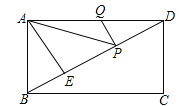
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.
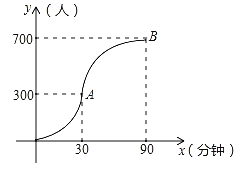
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为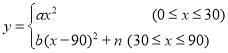 ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com