
光明文具厂工人的工作时间:每月26天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资920元,按月结算.该厂生产A,B两种型号零件,工人每生产一件A种型号零件,可得报酬0.85元,每生产一件B种型号零 件,可得报酬1.5元,下表记录的是工人小王的工作情况:
件,可得报酬1.5元,下表记录的是工人小王的工作情况:
生产A种型号零件/件 生产B种型号零件/件 总时间/分
2 2 70
6 4 170
根据上表提供的信息,请回答如下问题:
(1)小王每生产一件A种型号零件、每生产一 件B种型号零件,分别需要多少分钟?
件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目限制,那么小王该月的工资数目最多为多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是( )
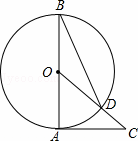
A. 30° B. 25° C. 20° D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
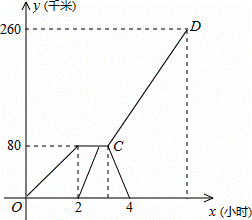
已知,A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
(1)甲车提速后的速度是 千米/时,乙车的速度是 千米/时,点C的坐标为 ;
(2)求乙车返回时y与x的函数关系式并写出自变量x的取值范围;
(3)求甲车到达B市时乙车已返回A市多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
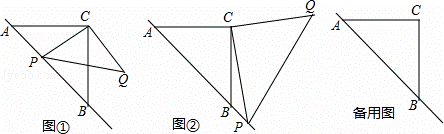
已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+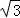 ,PA=
,PA=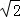 ,则:
,则:
①线段PB= 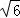 ,PC= 2 ;
,PC= 2 ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 PA2+PB2=PQ2 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足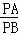 =
=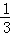 ,求
,求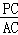 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com