
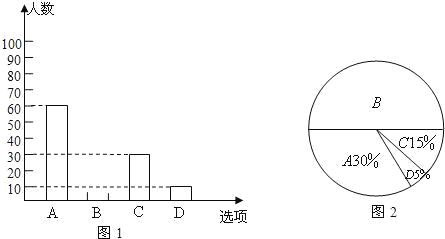
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A、1.5小时以上;B、1~1.5小时;C、0.5~1小时;D、0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下?
【答案】(1)200;(2)图形见解析;(3)学校有150人平均每天参加体育锻炼在0.5小时以下.
【解析】
(1)读图可得:A类有60人,占30%即可求得总人数;
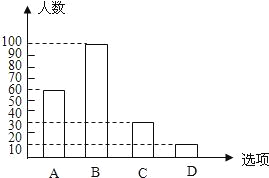
(2)计算可得:“B”是100人,据此补全条形图;
(3)用样本估计总体,若该校有3000名学生,则学校有3000×5%=150人平均每天参加体育锻炼在0.5小时以下.
解:(1)读图可得:A类有60人,占30%;则本次一共调查了60÷30%=200人;本次一共调查了200位学生;
(2)“B”有200-60-30-10=100人,画图正确;
(3)用样本估计总体,每天参加体育锻炼在0.5小时以下占5%;则3000×5%=150,
学校有150人平均每天参加体育锻炼在0.5小时以下.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元![]() 张,暑假为了促销,新推出两种优惠卡:
张,暑假为了促销,新推出两种优惠卡:
![]() 金卡售价600元
金卡售价600元![]() 张,每次凭卡不再收费.
张,每次凭卡不再收费.
![]() 银卡售价150元
银卡售价150元![]() 张,每次凭卡另收10元.
张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数![]() 设游泳x次时,所需总费用为y元
设游泳x次时,所需总费用为y元
![]() 分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
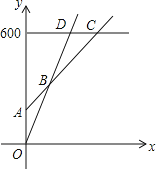
![]() 在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
![]() 请根据函数图象,直接写出选择哪种消费方式更合算.
请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数![]() 与摄氏度数
与摄氏度数![]() 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:
之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:
摄氏度数 | … | 0 | … | 35 | … | 100 | … |
华氏度数 | … | 32 | … | 95 | … | 212 | … |
(1)选用表格中给出的数据,求y关于x的函数解析式;
(2)有一种温度计上有两个刻度,即测量某一温度时左边是摄氏度,右边是华氏度,那么在多少摄氏度时,温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
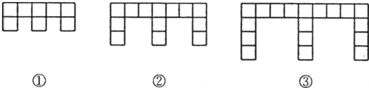
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动阳光体育活动的广泛开展,引导学生积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据图中提供的信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 人,图①中的m的值为 ,图①中“38号”所在的扇形的圆心角度数为 ;
(2)本次调查获取的样本数据的众数是 ,中位数是 ;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买36号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
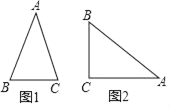
【题目】背景阅读:我们在教材24.3已经知道了直角三角形中锐角的三角函数的概念,类似地,我们在等腰三角形中建立边角之间的关系,即等腰三角形中底边与腰的比叫做顶角的正对,记作:sad.如图1,在△ABC中,AB=AC,顶角A的正对记作:sadA,这时sadA=![]() =
=![]() .
.
问题解决:
(1)若顶角A=60°,求sadA的值;
(2)若90°<∠A<180°,求∠A的正对sadA的取值范围;
合作交流:
(3)如图2,在Rt△ABC中,∠ACB=90°,若sinA=![]() ,试求以AC为腰的等腰三角形中,顶角A的正对sadA的值.
,试求以AC为腰的等腰三角形中,顶角A的正对sadA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞士著名数学家欧拉发现:简单多面体的顶点数V、面数F及棱数E之间满足一种有趣的关系:V+F﹣E=2,这个关系式被称为欧拉公式.比如:正二十面体(如右图),是由20个等边三角形所组成的正多面体,已知每个顶点处有5条棱,则可以通过欧拉公式算出正二十面体的顶点为_____个.那么一个多面体的每个面都是五边形,每个顶点引出的棱都有3条,它是一个_____面体.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com