
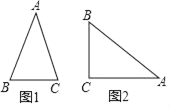
����Ŀ�������Ķ��������ڽ̲�24.3�Ѿ�֪����ֱ������������ǵ����Ǻ����ĸ�����Ƶأ������ڵ����������н����߽�֮��Ĺ�ϵ���������������еױ������ıȽ������ǵ����ԣ�������sad����ͼ1������ABC�У�AB=AC������A�����Լ�����sadA����ʱsadA=![]() =
=![]() ��
��
��������
��1��������A=60������sadA��ֵ��
��2����90�㣼��A��180�������A������sadA��ȡֵ��Χ��
����������
��3����ͼ2����Rt��ABC�У���ACB=90������sinA=![]() ��������ACΪ���ĵ����������У�����A������sadA��ֵ��
��������ACΪ���ĵ����������У�����A������sadA��ֵ��
���𰸡���1��1����2��![]() ��sad��BAC��2����3��
��sad��BAC��2����3��![]() .
.
����������������1�����жϳ���ABC�ǵȱ��������������ó�BC=AC�����ɵó�������
��2�����жϳ�![]() ��sin��BAD��1�������ó�
��sin��BAD��1�������ó�![]() ��
��![]() ��2�����ɵó�������
��2�����ɵó�������
��3�������BC=3a���ó�AB=5a��AC=4a�������ó�AE=AC=4a�����жϳ���AEF�ס�ABC���ó�EF=![]() a��AF=
a��AF=![]() a��������ʾ��CF=AC��AF=
a��������ʾ��CF=AC��AF=![]() a�����ù��ɶ����ó�CE=
a�����ù��ɶ����ó�CE=![]() a���ɵó����ۣ�
a���ɵó����ۣ�
�������1���ߵ��������εĶ���A=60�㣬���ABC�ǵȱ�����������BC=AC����sadA=![]() =1��
=1��
��2�����ͼ2������A��AD��BC��D����AB=AC����BC=2BD����90������BAC��180�㣬��45������BAD��90�㣬��![]() ��sin��BAD��1����Rt��ABD����sin��BAD=
��sin��BAD��1����Rt��ABD����sin��BAD=![]() ��
��![]() ��1����
��1����![]() ��
��![]() ��2����
��2����![]() ��
��![]() ��2���ڵ�����ABC����sad��BAC=
��2���ڵ�����ABC����sad��BAC=![]() ��sad��BAC��2��
��sad��BAC��2��
��3�����ͼ3����Rt��ABC����sinA=![]() =
=![]() ����BC=3a����AB=5a�����ݹ��ɶ�������AC=4a����AE=AC=4a������E��EF��AC��F���ߡ�ACB=90�㣬��EF��BC�����AEF�ס�ABC����
����BC=3a����AB=5a�����ݹ��ɶ�������AC=4a����AE=AC=4a������E��EF��AC��F���ߡ�ACB=90�㣬��EF��BC�����AEF�ס�ABC����![]() ����EF=
����EF=![]() a��AF=
a��AF=![]() a����CF=AC��AF=
a����CF=AC��AF=![]() a����Rt��CEF����CE=
a����Rt��CEF����CE=![]() =
=![]() a����sadA=
a����sadA=![]() =
=![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
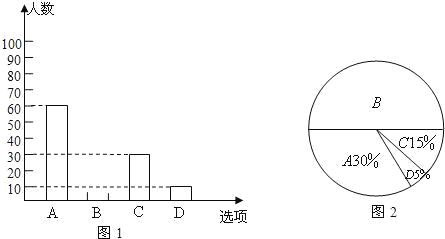
����Ŀ��ijУ��һ����ѧ��ȤС���ڱ�Уѧ���п�չ����Ϊ����������·���г�����Ѳ��������ר�������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����Ϊ���dz��˽��������Ƚ��˽������������˽���������̫�˽����ĸ��ȼ����ֱ����A��B��C��D�������ݵ��������Ƴ���ͼ��ʾ��������ͳ��ͼ������ͼ����Ϣ����������⣺

��1����������α������ѧ���������ˣ���������ͳ��ͼ����������
��2�����Ƹ�У1500��ѧ������C�ȼ�����ѧ���ж����ˣ�
��3������B�ȼ�����ѧ���У�����ѧ������4�ˣ�����1��3Ů������4�����У����ѡ��2�˽��вɷã�����ѡ��λͬѧ������ͬѧ�ĸ����Ƕ��٣������б�������״ͼ�ķ�����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ѧ���μ�������������ѧУ��ѧ����������������飬����һ������������ƽ��ÿ��μ��������ʱ���Ƕ�����������4��ѡ�A��1.5Сʱ���ϣ�B��1��1.5Сʱ��C��0.5��1Сʱ��D��0.5Сʱ���£�ͼ1��2�Ǹ��ݵ��������Ƶ�������������ͳ��ͼ���������ͳ��ͼ�ṩ����Ϣ������������⣺
��1������һ�������˶�����ѧ����
��2����ͼ1�н�ѡ��B�IJ��ֲ���������
��3������У��3000��ѧ���������ȫУ�����ж�����ѧ��ƽ��ÿ��μ��������ʱ����0.5Сʱ���£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ܰɣ��ֵܣ�����Ŀ�飬Ԥ���һ���µ���Ϸ����������·���辭A��B��C��D�ĵأ���ͼ������A��B��C������ͬһֱ���ϣ�D����A�ر�ƫ��30��������C�ر�ƫ��45������C����A�ر�ƫ��75��������BD=BC=30m����A�ص�D�صľ����ǣ�������

A. 30![]() m B. 20
m B. 20![]() m C. 30
m C. 30![]() m D. 15
m D. 15![]() m
m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����ϰ���֣���֪С����С��ÿ���Ӷ��80���֣�С����3500���ֵ�ʱ����С����2500���ֵ�ʱ����ͬ��
��1��С����С��ÿ���ӷֱ�ɴ�����֣�
��2�������һ��������Ϊm�ĸ����Ҫ������ԣ�С��������![]() ��Сʱ�����µ����빤����С��������ɣ���С������Ҫ��������Сʱ�������ý���ú���
��Сʱ�����µ����빤����С��������ɣ���С������Ҫ��������Сʱ�������ý���ú���![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() ��Ϊ�������������
���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A�������϶�Ӧ����Ϊa����B��Ӧ����Ϊb����|a+2|+��b��1��2=0��A��B֮��ľ������|AB|�����壺|AB|=|a��b|��
���߶�AB�ij�|AB|=3��
�����P�������϶�Ӧ����Ϊx����|PA|��|PB|=2ʱ��x=0.5��
������P��A����࣬M��N�ֱ���PA��PB���е㣬��P��A������ƶ�ʱ|PM|+|PN|��ֵ���䣻
�������������£�|PN|��|PM|��ֵ���䣮
�����٢ڢۢ���������ȷ����_______������������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��ͬѧ�����Ƶ�ֱ��������ֽ��DEF������AB�ĸ߶ȣ��������Լ���λ�ã��跨ʹб��DF����ˮƽ�����ұ�DE���B��ͬһֱ���ϣ���ֽ֪�������ֱ�DZ�DE��40cm��EF��20cm����ñ�DF�����ĸ߶�AC��1.5m��CD��8m������AB�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
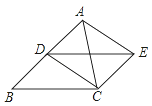
����Ŀ����֪����ͼ����D����ABC�ı�AB���е㣬�ı���BCED��ƽ���ı��Σ�
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2������ABC����ʲô����ʱ��ƽ���ı���ADCE�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ![]() �ij�������a��������b����a��b��������������Ӧ�ĵ�ֱ�ΪA��B������A����Bͬʱ���������������˶�����A���ٶ��ǵ�B��2������3���
�ij�������a��������b����a��b��������������Ӧ�ĵ�ֱ�ΪA��B������A����Bͬʱ���������������˶�����A���ٶ��ǵ�B��2������3���![]() �����B���ٶ�Ϊ�� ��
�����B���ٶ�Ϊ�� ��
A.![]() B.
B.![]() ��
�� ![]() C.
C.![]() ��
��![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com