
ЁОЬтФПЁПвбжЊЕуAдкЪ§жсЩЯЖдгІЕФЪ§ЮЊaЃЌЕуBЖдгІЕФЪ§ЮЊbЃЌЧв|a+2|+ЃЈbЉ1ЃЉ2=0ЃЌAЁЂBжЎМфЕФОрРыМЧзї|AB|ЃЌЖЈвхЃК|AB|=|aЉb|ЃЎ
ЂйЯпЖЮABЕФГЄ|AB|=3ЃЛ
ЂкЩшЕуPдкЪ§жсЩЯЖдгІЕФЪ§ЮЊxЃЌЕБ|PA|Љ|PB|=2ЪБЃЌx=0.5ЃЛ
ЂлШєЕуPдкAЕФзѓВрЃЌMЁЂNЗжБ№ЪЧPAЁЂPBЕФжаЕуЃЌЕБPдкAЕФзѓВрвЦЖЏЪБ|PM|+|PN|ЕФжЕВЛБфЃЛ
ЂмдкЂлЕФЬѕМўЯТЃЌ|PN|Љ|PM|ЕФжЕВЛБфЃЎ
вдЩЯЂйЂкЂлЂмНсТлжае§ШЗЕФЪЧ_______ЃЈЬюЩЯЫљгае§ШЗНсТлЕФађКХЃЉ
ЁОД№АИЁПЂйЂкЂм
ЁОНтЮіЁПЃЈ1ЃЉИљОнЗЧИКЪ§ЕФКЭЮЊ0ЃЌИїЯюЖМЮЊ0ЃЛ
ЃЈ2ЃЉгІПМТЧЕНAЁЂBЁЂPШ§ЕужЎМфЕФЮЛжУЙиЯЕЕФЖржжПЩФмНтЬтЃЛ
ЃЈ3ЃЉ(4)РћгУжаЕуаджЪзЊЛЏЯпЖЮжЎМфЕФБЖЗжЙиЯЕЕУГіЃЎ
ЃЈ1ЃЉЁп|a+2|+ЃЈb-1ЃЉ2=0ЃЌ
Ёрa=-2ЃЌb=1ЃЌ
ЁрAB=|a-b|=3ЃЌМДЯпЖЮABЕФГЄЖШЮЊ3ЃЎ
ЃЈ2ЃЉЕБPдкЕуAзѓВрЪБЃЌ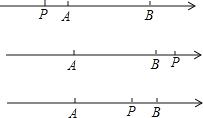
|PA|-|PB|=-ЃЈ|PB|-|PA|ЃЉ=-|AB|=-3Ёй2ЃЎ
ЕБPдкЕуBгвВрЪБЃЌ
|PA|-|PB|=|AB|=3Ёй2ЃЎ
ЁрЩЯЪіСНжжЧщПіЕФЕуPВЛДцдкЃЎ
ЕБPдкAЁЂBжЎМфЪБЃЌ-2ЁмxЁм1ЃЌ
Ёп|PA|=|x+2|=x+2ЃЌ|PB|=|x-1|=1-xЃЌ
ЁргЩ|PA|-|PB|=2ЃЌЕУx+2-ЃЈ1-xЃЉ=2ЃЎ
ЁрНтЕУЃКx=0.5ЃЛ
ЃЈ3ЃЉгЩвбжЊПЩЕУГіЃКPM=![]() PAЃЌPN=
PAЃЌPN=![]() PBЃЌ
PBЃЌ
|PM|+|PN|= ![]() ЃЈPA+PBЃЉ= PA+
ЃЈPA+PBЃЉ= PA+![]() AB
AB
ЫљвдЃЌ|PM|+|PN|ЕФжЕЫцPЕФЮЛжУБфЛЏЖјБфЛЏ.
(4) дкЃЈ3ЃЉЬѕМўЯТЃЌ|PN|Љ|PM|=![]() PB-
PB-![]() PA=
PA=![]() ЃЈPB-PAЃЉ=
ЃЈPB-PAЃЉ=![]() AB=
AB=![]()
злКЯЩЯЪіЃЌЂйЂкЂмЫЕЗЈе§ШЗ.
ЙЪД№АИЮЊЃКЂйЂкЂм.


 ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ
аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() дкЪ§жсЩЯЖдгІЕФЪ§ЮЊ
дкЪ§жсЩЯЖдгІЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЖдгІЕФЪ§ЮЊ
ЖдгІЕФЪ§ЮЊ![]() ЃЌЙигк
ЃЌЙигк![]() ЃЌ
ЃЌ![]() ЕФЖрЯюЪН
ЕФЖрЯюЪН![]() ЪЧ6ДЮЖрЯюЪНЃЌЧвГЃЪ§ЯюЮЊ-6.
ЪЧ6ДЮЖрЯюЪНЃЌЧвГЃЪ§ЯюЮЊ-6.
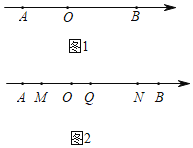
ЃЈ1ЃЉЕу![]() ЕН
ЕН![]() ЕФОрРыЮЊ______ЃЈжБНгаДГіНсЙћЃЉЃЛ
ЕФОрРыЮЊ______ЃЈжБНгаДГіНсЙћЃЉЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕу![]() ЪЧЪ§жсЩЯвЛЕуЃЌЕу
ЪЧЪ§жсЩЯвЛЕуЃЌЕу![]() ЕН
ЕН![]() ЕФОрРыЪЧ
ЕФОрРыЪЧ![]() ЕН
ЕН![]() ЕФОрРыЕФ3БЖЃЈМД
ЕФОрРыЕФ3БЖЃЈМД![]() ЃЉЃЌЧѓЕу
ЃЉЃЌЧѓЕу![]() дкЪ§жсЩЯЖдгІЕФЪ§ЃЛ
дкЪ§жсЩЯЖдгІЕФЪ§ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ДгЕу
ЗжБ№ДгЕу![]() ЃЌ
ЃЌ![]() ЭЌЪБГіЗЂЃЌЗжБ№вд
ЭЌЪБГіЗЂЃЌЗжБ№вд![]() ЃЌ
ЃЌ![]() ЕФЫйЖШбиЪ§жсИКЗНЯђдЫЖЏЃЈ
ЕФЫйЖШбиЪ§жсИКЗНЯђдЫЖЏЃЈ![]() дк
дк![]() ЃЌ
ЃЌ![]() жЎМфЃЌ
жЎМфЃЌ![]() дк
дк![]() ЃЌ
ЃЌ![]() жЎМфЃЉЃЌдЫЖЏЪБМфЮЊ
жЎМфЃЉЃЌдЫЖЏЪБМфЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЃЌ
ЃЌ![]() жЎМфвЛЕуЃЌЧвЕу
жЎМфвЛЕуЃЌЧвЕу![]() ЕН
ЕН![]() ЕФОрРыЪЧЕу
ЕФОрРыЪЧЕу![]() ЕН
ЕН![]() ОрРыЕФвЛАыЃЈМД
ОрРыЕФвЛАыЃЈМД![]() ЃЉЃЌШє
ЃЉЃЌШє![]() ЃЌ
ЃЌ![]() дЫЖЏЙ§ГЬжа
дЫЖЏЙ§ГЬжа![]() ЕН
ЕН![]() ЕФОрРыЃЈМД
ЕФОрРыЃЈМД![]() ЃЉзмЮЊвЛИіЙЬЖЈЕФжЕЃЌЧѓ
ЃЉзмЮЊвЛИіЙЬЖЈЕФжЕЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ10ЗжЃЉЯТУцЕФЭМаЮЪЧгЩБпГЄЮЊlЕФе§ЗНаЮАДееФГжжЙцТЩХХСаЖјзщГЩЕФЃЎ
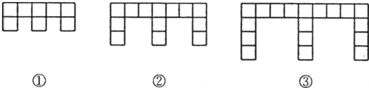
ЃЈ1ЃЉЙлВьЭМаЮЃЌЬюаДЯТБэЃК
ЭМаЮ | Ђй | Ђк | Ђл |
е§ЗНаЮЕФИіЪ§ | 8 | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЭМаЮЕФжмГЄ | 18 | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЃЈ2ЃЉЭЦВтЕкnИіЭМаЮжаЃЌе§ЗНаЮЕФИіЪ§ЮЊЁЁ ЁЁЃЌжмГЄЮЊЁЁ ЁЁЃЈЖМгУКЌnЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЃЈ3ЃЉетаЉЭМаЮжаЃЌШЮвтвЛИіЭМаЮЕФжмГЄyгыЫќЫљКЌе§ЗНаЮИіЪ§xжЎМфЕФЙиЯЕПЩБэЪОЮЊy=ЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁУїЯыгУОЕзгВтСПвЛПУЫЩЪїЕФИпЖШЃЌЕЋЪїХдгавЛЬѕКгЃЌВЛФмВтСПОЕзггыЪїжЎМфЕФОрРыЃЌгкЪЧаЁУїСНДЮРћгУОЕзгЃЌЕквЛДЮЫћАбОЕзгЗХдкCЕуЃЌШЫдкFЕуе§КУдкОЕзгжаПДМћЪїМтAЃЛЕкЖўДЮАбОЕзгЗХдкDЕуЃЌШЫдкHЕуе§КУдкОЕзгжаПДЕНЪїМтAЃЎвбжЊаЁУїЕФблОІОрРыЕиУцЕФОрРыEF=1.68УзЃЌСПЕУCD=10УзЃЌCF=1.2УзЃЌDH=3.6УзЃЌРћгУетаЉЪ§ОнФуФмЧѓГіетПУЫЩЪїЕФИпЖШТ№ЃПЪдЪдПДЃЎЃЈгбЧщЬсЪОЃКЁЯACB=ЁЯECFЃЌЁЯADF=ЁЯGDHЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
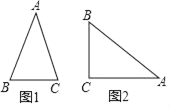
ЁОЬтФПЁПБГОАдФЖСЃКЮвУЧдкНЬВФ24.3вбОжЊЕРСЫжБНЧШ§НЧаЮжаШёНЧЕФШ§НЧКЏЪ§ЕФИХФюЃЌРрЫЦЕиЃЌЮвУЧдкЕШбќШ§НЧаЮжаНЈСЂБпНЧжЎМфЕФЙиЯЕЃЌМДЕШбќШ§НЧаЮжаЕзБпгыбќЕФБШНазіЖЅНЧЕФе§ЖдЃЌМЧзїЃКsadЃЎШчЭМ1ЃЌдкЁїABCжаЃЌAB=ACЃЌЖЅНЧAЕФе§ЖдМЧзїЃКsadAЃЌетЪБsadA=![]() =
=![]() ЃЎ
ЃЎ
ЮЪЬтНтОіЃК
ЃЈ1ЃЉШєЖЅНЧA=60ЁуЃЌЧѓsadAЕФжЕЃЛ
ЃЈ2ЃЉШє90ЁуЃМЁЯAЃМ180ЁуЃЌЧѓЁЯAЕФе§ЖдsadAЕФШЁжЕЗЖЮЇЃЛ
КЯзїНЛСїЃК
ЃЈ3ЃЉШчЭМ2ЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌШєsinA=![]() ЃЌЪдЧѓвдACЮЊбќЕФЕШбќШ§НЧаЮжаЃЌЖЅНЧAЕФе§ЖдsadAЕФжЕЃЎ
ЃЌЪдЧѓвдACЮЊбќЕФЕШбќШ§НЧаЮжаЃЌЖЅНЧAЕФе§ЖдsadAЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНk1xЃЋ1гыЫЋЧњЯпyЃН![]() ЯрНЛгкP(1ЃЌm)ЃЌQ(Ѓ2ЃЌЃ1)СНЕуЃЎ
ЯрНЛгкP(1ЃЌm)ЃЌQ(Ѓ2ЃЌЃ1)СНЕуЃЎ
(1)ЧѓmЕФжЕЃЛ
(2)ШєA1(x1ЃЌy1)ЃЌA2(x2ЃЌy2)ЃЌA3(x3ЃЌy3)ЮЊЫЋЧњЯпЩЯШ§ЕуЃЌЧвx1<x2<0<x3ЃЌЧыжБНгЫЕУїy1ЃЌy2ЃЌy3ЕФДѓаЁЙиЯЕЃЛ
(3)ЙлВьЭМЯѓЃЌЧыжБНгаДГіВЛЕШЪНk1xЃЋ1>![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЕиЯрОр300ЧЇУзЃЌвЛСОЛѕГЕКЭвЛСОНЮГЕЗжБ№ДгМзЕиПЊЭљввЕи![]() НЮГЕЕФЦНОљЫйЖШДѓгкЛѕГЕЕФЦНОљЫйЖШ
НЮГЕЕФЦНОљЫйЖШДѓгкЛѕГЕЕФЦНОљЫйЖШ![]() ЃЌШчЭМЃЌЯпЖЮOAЁЂелЯпBCDЗжБ№БэЪОСНГЕРыМзЕиЕФОрРы
ЃЌШчЭМЃЌЯпЖЮOAЁЂелЯпBCDЗжБ№БэЪОСНГЕРыМзЕиЕФОрРы![]() ЕЅЮЛЃКЧЇУз
ЕЅЮЛЃКЧЇУз![]() гыЪБМф
гыЪБМф![]() ЕЅЮЛЃКаЁЪБ
ЕЅЮЛЃКаЁЪБ![]() жЎМфЕФКЏЪ§ЙиЯЕЃЎ
жЎМфЕФКЏЪ§ЙиЯЕЃЎ
![]() ЯпЖЮOAгыелЯпBCDжаЃЌ______БэЪОЛѕГЕРыМзЕиЕФОрРыyгыЪБМфxжЎМфЕФКЏЪ§ЙиЯЕЃЎ
ЯпЖЮOAгыелЯпBCDжаЃЌ______БэЪОЛѕГЕРыМзЕиЕФОрРыyгыЪБМфxжЎМфЕФКЏЪ§ЙиЯЕЃЎ
![]() ЧѓЯпЖЮCDЕФКЏЪ§ЙиЯЕЪНЃЛ
ЧѓЯпЖЮCDЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ЛѕГЕГіЗЂЖрГЄЪБМфСНГЕЯргіЃП
ЛѕГЕГіЗЂЖрГЄЪБМфСНГЕЯргіЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШёНЧЁїABCФкНггкЁбOЃЌШєЁбOЕФАыОЖЮЊ6ЃЌsinA=![]() ЃЌЧѓBCЕФГЄЃЎ
ЃЌЧѓBCЕФГЄЃЎ

ЁОД№АИЁПBC=8ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЭЈЙ§зїИЈжњЯпЙЙГЩжБНЧШ§НЧаЮЃЌдйРћгУШ§НЧКЏЪ§жЊЪЖНјааЧѓНтЃЎ
ЪдЬтНтЮіЃКзїЁбOЕФжБОЖCDЃЌСЌНгBDЃЌдђCD=2ЁС6=12.
Ёп![]()
Ёр![]()
Ёр![]()

ЕуОІЃКжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
22
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=k1x+bгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ2ЃЉСНЕуЃЎЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊCЃЌЧвSЁїABC=5ЃЎ
ЕФЭМЯѓНЛгкAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ2ЃЉСНЕуЃЎЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊCЃЌЧвSЁїABC=5ЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЫљИјЬѕМўЃЌЧыжБНгаДГіВЛЕШЪНk1x+bЃО![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉШєPЃЈpЃЌy1ЃЉЃЌQЃЈЉ2ЃЌy2ЃЉЪЧКЏЪ§y=![]() ЭМЯѓЩЯЕФСНЕуЃЌЧвy1Ёнy2ЃЌЧѓЪЕЪ§pЕФШЁжЕЗЖЮЇЃЎ
ЭМЯѓЩЯЕФСНЕуЃЌЧвy1Ёнy2ЃЌЧѓЪЕЪ§pЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКbЪЧзюаЁЕФе§ећЪ§ЧвaЁЂbТњзу![]() ЃЌЪдЛиД№ЮЪЬт.
ЃЌЪдЛиД№ЮЪЬт.
ЃЈ1ЃЉЧыжБНгаДГіaЁЂbЁЂcЕФжЕ.
a= b= c= .
ЃЈ2ЃЉaЁЂbЁЂcЫљЖдгІЕФЕуЗжБ№ЮЊAЁЂBЁЂCЃЌЕуPЮЊвЛЖЏЕуЃЌЦфЖдгІЕФЪ§ЮЊxЃЌЕуPдк0ЕН2жЎМфдЫЖЏЪБЃЈМД0ЁмxЁм2ЪБЃЉЃЌЧыЛЏМђЪНзгЃК![]() ЃЈЧыаДГіЛЏМђЙ§ГЬЃЉ
ЃЈЧыаДГіЛЏМђЙ§ГЬЃЉ
![]()
ЃЈ3ЃЉдкЃЈ1ЃЉЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЕуDДгAЕуПЊЪМвдУПУы1ЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЕуEДгBЕуПЊЪМвдУПУы2ИіЕЅЮЛГЄЖШЯђгвдЫЖЏЃЌЕуFДгCЕуПЊЪМвдУПУы5ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌЩшЫќУЧдЫЖЏЕФtУыЃЌЧыЮЪЃЌEFЉDEЕФжЕЪЧЗёЫцзХЪБМфtЕФБфЛЏЖјБфЛЏЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыЧѓЦфжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com