
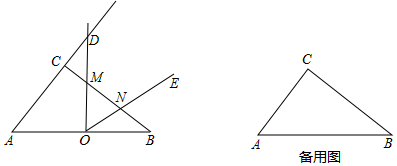
分析 (1)如图1中,作OH⊥BC于H.只要证明△DCM≌△OHM,即可得出CD=OH=3.
(2)如图2中,作NG⊥OB于G.首先证明∠1=∠2,根据tan∠1=tan∠2,可得$\frac{MH}{OH}$=$\frac{NG}{OG}$,由此即可解决问题.
(3)分两种情形讨论即可①如图3中,当OM=ON时,OH垂直平分MN,②如图4中,当OM=MN时,分别求解即可.
解答 解:(1)如图1中,作OH⊥BC于H.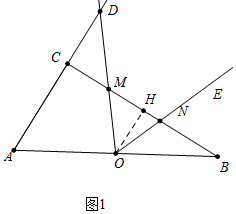
在Rt△ABC中,∵AB=10,sinB=$\frac{3}{5}$,
∴AC=6,BC=8,
∵AO=OB,OH∥AC,
∴CH=HB=4,OH=3,
∵CM=2,
∴CM=HM=2,
在△DCM和△OHM中,
$\left\{\begin{array}{l}{∠CMD=∠OMH}\\{∠DCM=∠OHM=90°}\\{CM=MH}\end{array}\right.$,
∴△DCM≌△OHM,
∴CD=OH=3.
(2)如图2中,作NG⊥OB于G.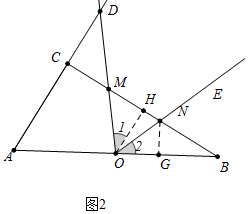
∵∠HOB=∠A=∠MON,
∴∠1=∠2,
在Rt△BNG中,BN=y,sibB=$\frac{3}{5}$,
∴GN=$\frac{3}{5}$y,BG=$\frac{4}{5}$y,
∵tan∠1=tan∠2,
∴$\frac{MH}{OH}$=$\frac{NG}{OG}$,
∴$\frac{4-x}{3}$=$\frac{\frac{3}{5}y}{5-\frac{4}{5}y}$,
∴y=$\frac{100-25x}{25-4x}$,(0<x<4).
(3)①如图3中,当OM=ON时,OH垂直平分MN,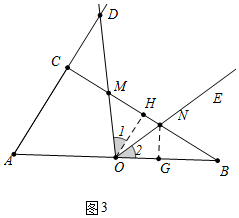
∴BN=CM=x,
∵△OMH≌△ONG,
∴NG=HM=4-x,
∵sinB=$\frac{3}{5}$,
∴$\frac{4-x}{x}$=$\frac{3}{5}$,
∴CM=x=$\frac{5}{2}$.
②如图4中,当OM=MN时.连接CO,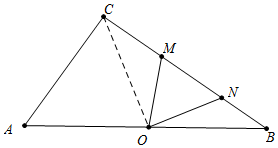
∵OA=OB,OM=MN,
∴CO=OA=OB,
∴∠MON=∠MNO=∠A=∠OCA,
∴△MON∽△OAC,
∴∠AOC=∠OMN,
∴∠BOC=∠CMO,∵∠B=∠B,
∴△CMO∽△COB,
∴$\frac{CO}{CB}$=$\frac{CM}{CO}$,
∴8x=52,
∴x=$\frac{25}{8}$.
综上所述,△OMN是以OM为腰的等腰三角形时,线段CM的长为$\frac{5}{2}$或$\frac{25}{8}$.
点评 本题考查几何变换综合题、全等三角形的判定和性质、锐角三角函数、相似三角形的判定和性质等知识,解题的关键是灵活应用所学知识解决问题,学会添加常用辅助线,构造相似三角形或全等三角形,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
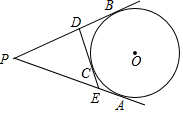 如图,PA、PB、DE分别切⊙O于A、B、C,如果PA=8cm,那么△PDE的周长是( )
如图,PA、PB、DE分别切⊙O于A、B、C,如果PA=8cm,那么△PDE的周长是( )| A. | 16cm | B. | 32cm | C. | 17cm | D. | 15cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△OAB是等边三角形,边长为12,AB⊥y轴于C.
如图,△OAB是等边三角形,边长为12,AB⊥y轴于C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com