
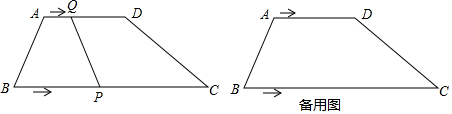
���� ��1�������˶��ó�PC=26-3t��DQ=16-t��������ƽ���ı��εĶԱ���Ƚ���������⼴�ɣ�
��2����������εĸ�DH���ٷ�������������ε��������������⼴�ɣ�
��3���ֵ�P�Ǵӵ�B���C�˶��Ĺ����к͵�P�����C���ص�Bʱ��ÿ������ֵַ�DΪֱ�Ƕ���͵�PΪֱ�Ƕ��㣬�ù��ɶ������ɵó����ۣ�
��� �⣺��1�����˶�֪��BP=3t��AQ=t��
��BC=26cm��AD=16cm��
��PC=26-3t��DQ=16-t��
���ı���PQDC��ƽ���ı��Σ���AD��BC��
��PC=DQ��
��26-3t=16-t��
��t=5��
����t=5��ʱ���ı���PQDC��ƽ���ı��Σ�
��2������D��DH��BC��
��Rt��CDH�У���BCD=30�㣬CD=8��
��DH=4��CH=4$\sqrt{3}$��
��ͼ����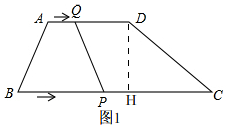 ����P�Ǵӵ�B���C�˶���
����P�Ǵӵ�B���C�˶���
�ɣ�1��֪��PC=26-3t��DQ=16-t��
����C��D��Q��PΪ������ı����������36cm2��
��S�ı���CDQP=$\frac{1}{2}$��DQ+CP����DH=$\frac{1}{2}$��16-t+26-3t����4=36��
��t=6���ڵ���P�Ǵӵ�C���ص�Bʱ��
���˶�֪��DQ=16-t��CP=3t-26��
����C��D��Q��PΪ������ı����������36cm2��
��S�ı���CDQP=$\frac{1}{2}$��DQ+CP����DH=$\frac{1}{2}$��16-t+3t-26����4=36��
��t=14���൱tΪ6���14��ʱ����C��D��Q��PΪ������ı����������36cm2��
��3���ٵ���P�ӵ�B���C�˶�ʱ��
�ߡ�PCD��ֱ�������Σ�
��D��ֱ�Ƕ��㣬��ͼ2��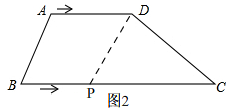 ��Rt��CDP�У���BCD=30�㣬CD=8��
��Rt��CDP�У���BCD=30�㣬CD=8��
��cos30��=$\frac{CD}{CP}$��
��CP=$\frac{CD}{cos30��}$=$\frac{16\sqrt{3}}{3}$��
��26-3t=$\frac{16\sqrt{3}}{3}$��
��t=$\frac{26}{3}-\frac{16\sqrt{3}}{9}$��
����PΪֱ�Ƕ���ʱ����ͼ3��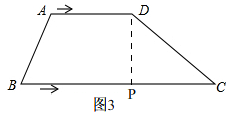 ��Rt��CPD�У���BCD=30�㣬CD=8��
��Rt��CPD�У���BCD=30�㣬CD=8��
��CP=4$\sqrt{3}$��
��26-3t=4$\sqrt{3}$��
��t=$\frac{26}{3}-\frac{4\sqrt{3}}{3}$��
�ڵ���P�Ǵӵ�C���ص�Bʱ��
����DΪֱ�Ƕ���ʱ��CP=3t-26=$\frac{16\sqrt{3}}{3}$��
��t=$\frac{26}{3}+\frac{16\sqrt{3}}{9}$��
����PΪֱ�Ƕ���ʱ��CP=3t-26=4$\sqrt{3}$��
��t=$\frac{26}{3}+\frac{4\sqrt{3}}{3}$��
������PCD��ֱ��������ʱ��t��ֵΪ$\frac{26}{3}-\frac{16\sqrt{3}}{9}$��$\frac{26}{3}-\frac{4\sqrt{3}}{3}$��$\frac{26}{3}+\frac{4\sqrt{3}}{3}$��$\frac{26}{3}+\frac{16\sqrt{3}}{9}$��
���� �������ı����ۺ��⣬��Ҫ������ֱ�������ε����ʣ����ɶ��������ε������ʽ���÷��̵�˼���ǽⱾ��Ĺؼ�����һ���е��Ѷȵ��п������⣮


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | AB=5��BC=6��AC=13 | B�� | AB=8��BC=8����A=40�� | ||
| C�� | ��A=60�㣬��B=45�㣬BC=4 | D�� | ��C=90�㣬AB=12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
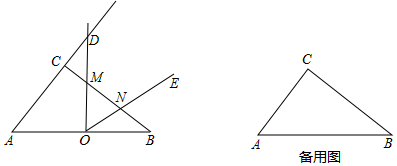
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ɼ� | Ƶ�� | �ٷֱ� |
| ������ | 9 | 10% |
| ���� | 18 | 20% |
| ���� | 36 | 40% |
| ���� | 27 | 30% |
| �ϼ� | 90 | 100% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
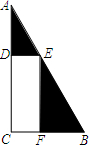 ��������һ��ֱ�������β˵��Ͽ��ٳ�һ����β˵���ֲ���ˣ�ʣ��˵���ֲ�ײˣ���ͼ����֪��ACB=90�㣬AB=50m����ֲ���˵ľ��β˵�CDEF����3������ֱ���AC��AB��BC�ϣ���CD�ij���Ϊx m������CDEF�����Ϊy m2��
��������һ��ֱ�������β˵��Ͽ��ٳ�һ����β˵���ֲ���ˣ�ʣ��˵���ֲ�ײˣ���ͼ����֪��ACB=90�㣬AB=50m����ֲ���˵ľ��β˵�CDEF����3������ֱ���AC��AB��BC�ϣ���CD�ij���Ϊx m������CDEF�����Ϊy m2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
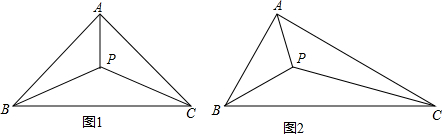
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3m | B�� | 3m-3 | C�� | $\frac{m+3}{3}$ | D�� | 3m-12 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com