

分析 (1)由SAS证明△ABA1≌△CBC1,即可得出结论;
(2)根据旋转的性质得∠A1C1B=∠ACB=45°,BC=BC1,利用等腰三角形的性质得∠CC1B=∠C1CB=45°,于是得到∠CC1A1=∠CC1B+∠A1C1B=90°;
(3)如图1,过点B作BD⊥AC,D为垂足,则点D在线段AC上,在Rt△BCD中利用三角函数可计算出BD=,则当BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值=EP1=BP1-BE;当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,如图2,EP1最大,最大值=EP1=BC+BE.
解答 (1)证明:∵将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
∴A1B=AB,C1B=CB,∠A1BC1=∠ABC,
∴∠A1BA=∠C1BC,
∵AB=BC,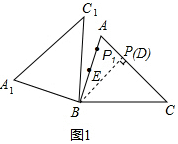
∴A1B=AB=C1B=CB,
在△ABA1和△CBC1中,$\left\{\begin{array}{l}{{A}_{1}B=B{C}_{1}}&{\;}\\{∠{A}_{1}BA=∠{C}_{1}BC}&{\;}\\{AB=BC}&{\;}\end{array}\right.$,
∴△ABA1≌△CBC1(SAS),
∴AA1=CC1;
(2)解:由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°;
(3)解:如图1,过点B作BD⊥AC,D为垂足,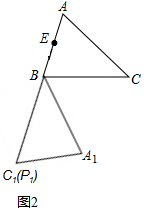
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,
最小值为:EP1=BP1-BE=BD-BE=2$\sqrt{2}$-$\frac{3}{2}$;
当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,
如图2,EP1最大,最大值为:EP1=BC+BE=4+$\frac{3}{2}$=$\frac{11}{2}$.
点评 本题是三角形综合题目,考查了全等三角形的判定与性质、旋转的性质、三角函数以及最大值与最小值问题;本题综合性强,有一定难度,熟练掌握旋转的性质,证明三角形全等是解决问题的关键:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.


科目:初中数学 来源: 题型:选择题
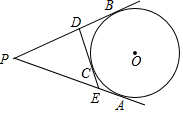 如图,PA、PB、DE分别切⊙O于A、B、C,如果PA=8cm,那么△PDE的周长是( )
如图,PA、PB、DE分别切⊙O于A、B、C,如果PA=8cm,那么△PDE的周长是( )| A. | 16cm | B. | 32cm | C. | 17cm | D. | 15cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
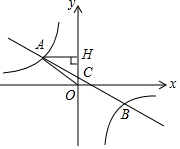 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交与第二、四象限内的A、B两点,与y轴交于C点.过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交与第二、四象限内的A、B两点,与y轴交于C点.过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△OAB是等边三角形,边长为12,AB⊥y轴于C.
如图,△OAB是等边三角形,边长为12,AB⊥y轴于C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com