
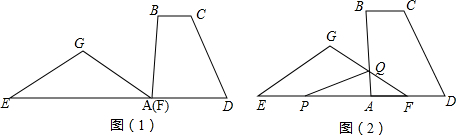
分析 (1)如图1,先作高线GH,利用等腰三角形三线合一可知:GH也是底边的中线,由顶角为120度,得两个底角为30°,依次求出EF和GH的长,代入面积公式可求面积;
如图2,当G点落在CD上时,依次求出DG、DF、AD的长,移动的路程为AF,与速度的商就是时间x;
(2)分三种情况讨论:①当0≤x≤2时,如图3,重叠部分的面积为△AFM的面积,②当2<x≤$\frac{10}{3}$时,如图4,重叠部分的面积为五边形GMADN的面积,利用面积差求重叠部分的面积;③当$\frac{10}{3}$<x≤4时,如图5,重叠部分的面积为四边形ADNM的面积,同理可求得面积;
(3)有两种情况:
①如图6,当PQ=FQ时,△FPQ是等腰三角形,根据AP+EP+AF=EF列式求得x,②如图7,当FQ=PF时,△FPQ是等腰三角形,同理列式可得结论.
解答 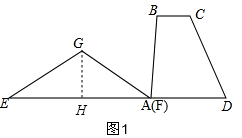 解:(1)如图1,过G作GH⊥EF于H,
解:(1)如图1,过G作GH⊥EF于H,
∵GE=GF,∠EGF=120°,
∴EH=FH,∠GEF=∠GFE=30°,
∵GE=4,
∴GH=$\frac{1}{2}$EG=2,
∴EH=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴EF=2EH=4$\sqrt{3}$,
∴S△EGF=$\frac{1}{2}$EF•GH=$\frac{1}{2}$×$4\sqrt{3}$×2=4$\sqrt{3}$;
如图2,当G点落在CD上时,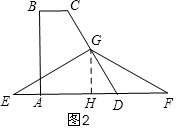
在Rt△DGH中,tan∠ADC=tan60°=$\frac{GH}{DH}$,
∴DH=$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$,
∴DG=2DH=$\frac{4\sqrt{3}}{3}$,
∵∠ADC=60°,∠F=30°,
∴∠DGF=30°,
∴DG=DF=$\frac{4\sqrt{3}}{3}$,
∴AF=AD+DF=$\frac{1}{2}$EF+DF=2$\sqrt{3}$+$\frac{4\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$,
∴x=$\frac{\frac{10\sqrt{3}}{3}}{\sqrt{3}}$=$\frac{10}{3}$,
故答案为:4$\sqrt{3}$;$\frac{10}{3}$秒;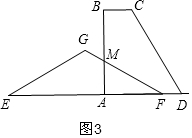
(2)分三种情况讨论:
①当0≤x≤2时,如图3,重叠部分的面积为△AFM的面积,
由题意得:AF=$\sqrt{3}$x,
在Rt△AFM中,∠GFE=30°,
tan30°=$\frac{AM}{AF}$,
∴AM=AF•tan30°=$\sqrt{3}$x•$\frac{\sqrt{3}}{3}$=x,
∴S=S△AFM=$\frac{1}{2}$AF•AM=$\frac{1}{2}$$•\sqrt{3}$x•x=$\frac{\sqrt{3}}{2}{x}^{2}$;
②当2<x≤$\frac{10}{3}$时,如图4,重叠部分的面积为五边形GMADN的面积,
过N作NH⊥AD于H,
∵AF=$\sqrt{3}$x,
∴AE=4$\sqrt{3}$-$\sqrt{3}$x,FD=AF-AD=$\sqrt{3}$x-2$\sqrt{3}$,
同(1)得:DN=FD=$\sqrt{3}$x-2$\sqrt{3}$,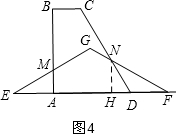
在Rt△AEM中,∠E=30°,
tan30°=$\frac{AM}{AE}$,
∴AM=$\frac{\sqrt{3}}{3}$(4$\sqrt{3}$-$\sqrt{3}$x)=4-x,
在Rt△DHN中,∠ADC=60°,
sin60°=$\frac{NH}{DN}$,
NH=$\frac{\sqrt{3}}{2}$×($\sqrt{3}$x-2$\sqrt{3}$)=$\frac{3}{2}x$-3,
∴S=S△GEF-S△AEM-S△DFN=4$\sqrt{3}$-$\frac{1}{2}$(4$\sqrt{3}$-$\sqrt{3}$x)(4-x)-$\frac{1}{2}$($\sqrt{3}$x-2$\sqrt{3}$)($\frac{3}{2}$x-3),
∴S=-$\frac{5\sqrt{3}}{4}{x}^{2}$+7$\sqrt{3}$x-7$\sqrt{3}$;
③当$\frac{10}{3}$<x≤4时,如图5,重叠部分的面积为四边形ADNM的面积,
AE=4$\sqrt{3}$-$\sqrt{3}$x,AM=4-x,
∴ED=AD+AE=2$\sqrt{3}$+4$\sqrt{3}$-$\sqrt{3}$x=6$\sqrt{3}$-$\sqrt{3}$x,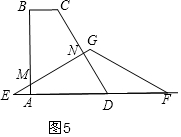
∵∠E=30°,∠ADC=60°,
∴∠END=90°,
∴DN=$\frac{1}{2}$ED=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x,
cos30°=$\frac{EN}{ED}$,
∴EN=$\frac{\sqrt{3}}{2}$(6$\sqrt{3}$-$\sqrt{3}$x)=9-$\frac{3}{2}$x,
∴S=S△END-S△AEM,
=$\frac{1}{2}$DN•EN-$\frac{1}{2}$AE•AM,
=$\frac{1}{2}$(3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x)(9-$\frac{3}{2}$x)-$\frac{1}{2}$(4$\sqrt{3}$-$\sqrt{3}$x)(4-x),
=-$\frac{\sqrt{3}}{8}{x}^{2}-\frac{\sqrt{3}}{2}x+\frac{11\sqrt{3}}{2}$;
综上所述,S与x的函数关系式为:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}^{2}(0≤x≤2)}\\{-\frac{5\sqrt{3}}{4}{x}^{2}+7\sqrt{3}x-7\sqrt{3}(2<x≤\frac{10}{3})}\\{-\frac{\sqrt{3}}{8}{x}^{2}-\frac{\sqrt{3}}{2}x+\frac{11\sqrt{3}}{2}(\frac{10}{3}<x≤4)}\end{array}\right.$;
(3)当0<x<2时,△FPQ可以成为等腰三角形,
有两种情况:
①如图6,当PQ=FQ时,△FPQ是等腰三角形,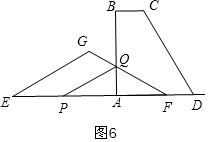
∴∠QPF=∠QFP=30°,
∵AQ⊥FE,
∴AP=AF=$\sqrt{3}$x,
由题意得:EP=$\sqrt{3}$x,
∴AP=EP=AF=$\sqrt{3}$x,
则3$\sqrt{3}$x=4$\sqrt{3}$,
x=$\frac{4}{3}$;
②如图7,当FQ=PF时,△FPQ是等腰三角形,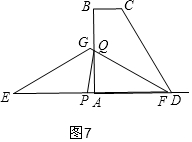
AF=EP=$\sqrt{3}$x,
cos30°=$\frac{AF}{FQ}$,
∴FQ=$\frac{AF}{cos30°}$=$\frac{\sqrt{3}x}{\frac{\sqrt{3}}{2}}$=2x,
∴PF=2x,
∴EF=PE+PF,
∴$\sqrt{3}$x+2x=4$\sqrt{3}$,
x=$\frac{4\sqrt{3}}{2+\sqrt{3}}$=4$\sqrt{3}$(2-$\sqrt{3}$)=8$\sqrt{3}$-12,
综上所述,当△FPQ是等腰三角形时,运动时间x的值为$\frac{4}{3}$秒或(8$\sqrt{3}$-12)秒.
点评 本题是四边形的综合题,考查了直角梯形、等腰三角形的性质和判定、平移的几何变换,本题比较复杂,首先要弄清动点运用的路线、速度、时间及路程,对于重叠部分面积的求法,要先找出特殊位置时所对应的时间,分情况进行求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
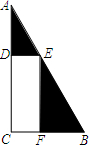 王大伯准备在一块直角三角形菜地上开辟出一块矩形菜地种植菠菜,剩余菜地种植白菜,如图.已知∠ACB=90°,AB=50m,种植菠菜的矩形菜地CDEF的另3个顶点分别在AC,AB,BC上,设CD的长度为x m,矩形CDEF的面积为y m2.
王大伯准备在一块直角三角形菜地上开辟出一块矩形菜地种植菠菜,剩余菜地种植白菜,如图.已知∠ACB=90°,AB=50m,种植菠菜的矩形菜地CDEF的另3个顶点分别在AC,AB,BC上,设CD的长度为x m,矩形CDEF的面积为y m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
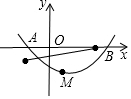 已知抛物线y=$\frac{1}{6}$(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,M为抛物线的顶点,设动点N(-2,n),求MN+BN的值最小时n的值.
已知抛物线y=$\frac{1}{6}$(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,M为抛物线的顶点,设动点N(-2,n),求MN+BN的值最小时n的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com