
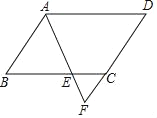
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 边上,
边上,![]() 的延长线交于点
的延长线交于点![]() ,下列结论错误的是( )
,下列结论错误的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据平行四边形的性质得出AD=BC,AD∥BC,AB∥CD,根据相似三角形的判定得出△FEC∽△FAD,△AEB∽△FEC,再根据相似三角形的性质得出比例式即可.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,AB∥CD,
A、∵BC∥AD,
∴△FEC∽△FAD,
∴![]() ,
,
∵AD=BC,
∴![]() ,正确,故本选项不符合题意;
,正确,故本选项不符合题意;
B、∵BC∥AD,
∴△FEC∽△FAD,
∴![]() ,
,
∵AD=BC,
∴![]() ,
,
∴![]() 错误,故本选项符合题意;
错误,故本选项符合题意;
C、∵BC∥AD,
∴△FEC∽△FAD,
∴![]() ,
,
∵AD=BC,
∴![]() ,正确,故本选项不符合题意;
,正确,故本选项不符合题意;
D、∵AB∥CD,
∴△AEB∽△FEC,
∴![]() ,正确,故本选项不符合题意;
,正确,故本选项不符合题意;
故选:B.


科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=![]() PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中数学 来源: 题型:
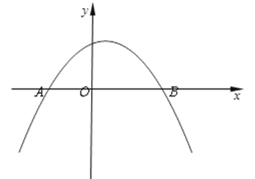
【题目】如图,已知平面直角坐标系![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于点A(-2,0)和点B(4,0) .
轴交于点A(-2,0)和点B(4,0) .
(1)求这条抛物线的表达式和对称轴;
(2)点C在线段OB上,过点C作CD⊥![]() 轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与
轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与![]() 轴交于点F.
轴交于点F.
①当D恰好是抛物线的顶点时,求点F的坐标;
②联结BF,当△DBC的面积是△BCF面积的![]() 时,求点C的坐标.
时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明研究一函数的性质,下表是该函数的几组对应值:

![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
![]() 根据所画函数图像,写出该函数的一条性质: .
根据所画函数图像,写出该函数的一条性质: .
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是 .
的范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
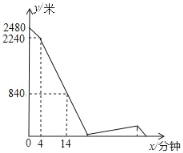
【题目】A、B两地之间的路程为2480米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是___米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒
轴以每秒![]() 个单位的速度向上移动,且过点
个单位的速度向上移动,且过点![]() 的直线
的直线![]() 也随之移动,如果点
也随之移动,如果点![]() 关于
关于![]() 的对称点落在坐标轴上,没点
的对称点落在坐标轴上,没点![]() 的移动时间为
的移动时间为![]() ,那么
,那么![]() 的值可以是___.
的值可以是___.
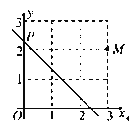
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
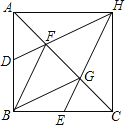
【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com