���𰸡�
��������1����������C�Ķ�����x����ʱ����=[-��m+1��]
2-4=0�����m��ֵ����������C�Ķ�����y����ʱ��-��m+1��=0�����m��ֵ�����ɵõ��𰸣�
��2����m��0ʱ��m=1�����ɵõ�������C�Ľ���ʽ������ƽ��n��n��0������λ��õ�y=x
2-2x+1-n������������y=x
2-2x+1-n��������C
1��y=ax
2+bx+c����y��Գƣ��õ�������C
1��y=x
2+2x+1-n���ѵ㣨n��3������������ɣ�
��3�����ڣ�������֪�����������C�Ľ���ʽ��y=x
2+1����P��������뼴�����P�����꣬����M��0��1������ֱ��x=-1�ĶԳƵ�M�䣨-2��1������ֱ��PM��Ľ���ʽΪy=kx+b����P��M����������õ������飬���������Ľ⼴�����Q�����꣮
�����1���⣺��������C�Ķ�����x����ʱ����=[-��m+1��]
2-4=0��
���m=1��m=-3��
��������C�Ķ�����y����ʱ��-��m+1��=0��
��m=-1��
����m=±1��m=-3��
��m��ֵ��m=±1��m=-3��
��2���⣺��m��0ʱ��m=1��
������C�Ľ���ʽΪy=x
2-2x+1��

����ƽ��n��n��0������λ��õ�y=x
2-2x+1-n��
������y=x
2-2x+1-n��������C
1��y=ax
2+bx+c����y��Գƣ�
��a=1��b=2��c=1-n��
��������C
1��y=x
2+2x+1-n��
��������C
1���㣨n��3��
��n
2+2n+1-n=3����n
2+n-2=0��
���n
1=1��n
2=-2��������n��0����ȥ����n=1
��������C
1��y=x
2+2x��
��C
1�ĺ�����ϵʽ��y=x
2+2x��
��3���⣺���ڣ������ǣ�
��-3��m��0ʱm=-1��
������C�Ľ���ʽ��y=x
2+1��
����M��0��1����
�߹���P��1��y
����
��y
=1+1=2��
��P��1��2����
����M��0��1������ֱ��x=-1�ĶԳƵ�M�䣨-2��1����
��ֱ��PM��Ľ���ʽΪy=kx+b��
��P��1��2����M�䣨-2��1������ã�
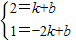
��
��ã�
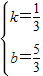
��
��ֱ��PM��Ľ���ʽΪ

��
��
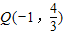
��
����ֱ��x=-1�ϴ���һ��Q��ʹ�á�QPM���ܳ���С����Q�������ǣ�-1��

����
������������Ҫ������ô���ϵ������һ�κ����Ľ���ʽ�����κ���ͼ���ϵ��������������һԪһ�η��̣����Ԫһ�η����飬���κ�������Y��ĵ�����꣬ƽ�Ƶ����ʵ�֪ʶ�����������գ��ۺ�������Щ���ʽ��м����ǽ����Ĺؼ���������һ���ۺ��Ժ�ǿ����Ŀ�����ͽϺã��Ѷ����У�


 ��
��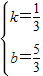 ��
�� ��
��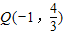 ��
�� ����
����


 �����ύ�ڵ�C�����x1��x2�Ƿ���x2-x-6=0����������x1��x2�����ҡ�ABC�����Ϊ
�����ύ�ڵ�C�����x1��x2�Ƿ���x2-x-6=0����������x1��x2�����ҡ�ABC�����Ϊ �������ҹ����ϵ��Ļ��Ų�����ͼ����ij���������͵�����ʾ��ͼ����֪�����ߵĺ�������ʽΪy=-
�������ҹ����ϵ��Ļ��Ų�����ͼ����ij���������͵�����ʾ��ͼ����֪�����ߵĺ�������ʽΪy=-