
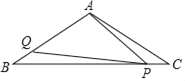
【题目】如图,已知△ABC中,AB=AC=![]() cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
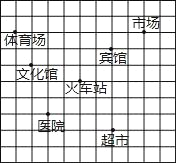
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系.
(2)写出市场的坐标为 ;超市的坐标为 .
(3)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.
解:因为,∠AOC:∠COD:∠BOD=2:3:4,
所以∠AOC= ,∠COD= ,∠BOD= ,
因为OE,OF分别平分∠AOC和∠BOD,
所以∠AOE= ,∠BOF= ,
所以∠EOF= ,
又因为 ,所以∠GOF=60°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABO的边长为2,O为坐标原点,A在 ![]() 轴上,B在第二象限。△ABO沿
轴上,B在第二象限。△ABO沿 ![]() 轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.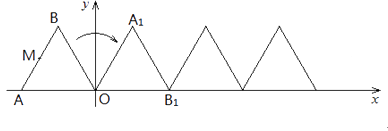
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】柯桥区某企业因为发展需要,从外地调运来一批94吨的原材料,现有甲、乙、丙三种车型共选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费6400元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象.下列说法错误的是( )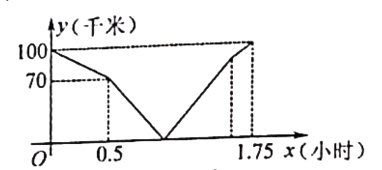
A.乙先出发的时间为0.5小时
B.甲的速度是80千米/小时
C.甲出发0.5小时后两车相遇
D.甲到B地比乙到A地早 ![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.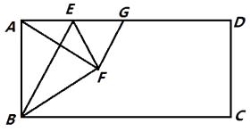
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示 ![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).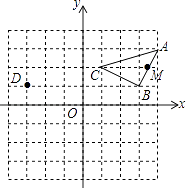
(1)点B和点C的坐标分别是、 .
(2)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF.
并直接写出E、F的坐标.
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com