
【题目】如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.
解:因为,∠AOC:∠COD:∠BOD=2:3:4,
所以∠AOC= ,∠COD= ,∠BOD= ,
因为OE,OF分别平分∠AOC和∠BOD,
所以∠AOE= ,∠BOF= ,
所以∠EOF= ,
又因为 ,所以∠GOF=60°.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
(Ⅰ)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(Ⅱ)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(Ⅲ)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是( )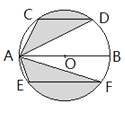
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
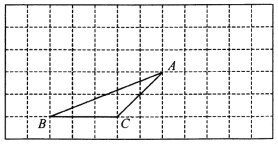
【题目】如图,方格纸中每个小正方形的边长为1个单位长度,三角形ABC的顶点都在格点上,将三角形ABC向右平移2个单位长度,再向上平移3个单位长度,得到三角形A′B′C′
(1)请在图中画出三角形A′B′C′;
(2)求三角形ABC的面积;
(3)若AC的长约为2.8,则边AC上的高约为多少?(结果保留分数)
查看答案和解析>>
科目:初中数学 来源: 题型:
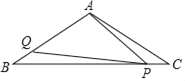
【题目】如图,已知△ABC中,AB=AC=![]() cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ//AB,则正方形EFGH的边长为.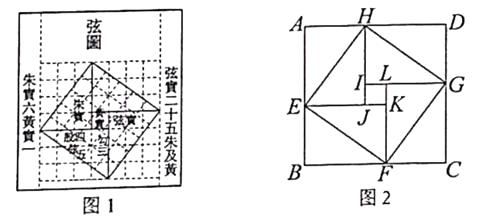
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com