
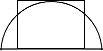
 如图,一个长为6,宽为5的长方形,和一个半径为5的半圆重合,则重合部分的面积最大为________.
如图,一个长为6,宽为5的长方形,和一个半径为5的半圆重合,则重合部分的面积最大为________.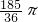
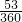 形OAB-S三角形ABO求出图形ABE、CDF的面积,最后用S半圆O-(图形ABE的面积+图形CDF的面积),得到重合部分最大的面积.
形OAB-S三角形ABO求出图形ABE、CDF的面积,最后用S半圆O-(图形ABE的面积+图形CDF的面积),得到重合部分最大的面积. 解:如图,连接OA、OD.
解:如图,连接OA、OD. π•52=
π•52= π.
π.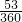 形OAB-S三角形ABO=×π•52-3×4÷2=
形OAB-S三角形ABO=×π•52-3×4÷2=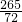 π-6.
π-6. π-2(
π-2(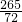 π-6)=12+
π-6)=12+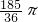 .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
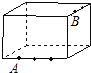 如图是一个长为8m,宽为6 m,高为5 m的仓库,在其内壁的点A(长的四等分点)处有一只壁虎.在点B(宽的三等分点)处有一只蚊子.则壁虎爬到蚊子处的最短距离应为( )
如图是一个长为8m,宽为6 m,高为5 m的仓库,在其内壁的点A(长的四等分点)处有一只壁虎.在点B(宽的三等分点)处有一只蚊子.则壁虎爬到蚊子处的最短距离应为( )A、
| ||
B、
| ||
C、5
| ||
| D、13m |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

| 9 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com