
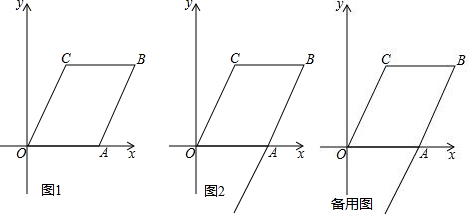
分析 (1)如图1,过点C作CD⊥OA于点D,解直角三角形求出OD、CD的长即可解决问题.
(2)分两种情形讨论即可①如图2中,当0≤t≤3时.②如图3中,当t>3时.分别想办法构建方程即可解决问题.
(3)分三种情形①如图4中,当0≤t≤3时.②当t>3时,由PB=QF时.③当点Q在y轴左侧时,构建PB=QF构建方程即可解决问题.
解答 解:(1)如图1,过点C作CD⊥OA于点D,
设菱形OABC的边长为x,则OA=OC=BC=x,
∵∠COA=60°,
∴CD=OC•sin60°=$\frac{\sqrt{3}}{2}$x,
∵菱形OABC的面积为18$\sqrt{3}$,
∴x•$\frac{\sqrt{3}}{2}$x=18$\sqrt{3}$,
解得:x=±6,
∴OA=OC=BC=6,
∴CD=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,OD=OC•cos60°=3,
∴点C的坐标为:(3,3$\sqrt{3}$),点B的坐标为:(9,3$\sqrt{3}$);
(2)①如图2中,当0≤t≤3时,作PK∥AB交AC于K,则△PCK是等边三角形.作DH⊥AB于H.
∵PK=PC=AQ,∠PDK=∠ADQ,∠KPD=∠DQA,
∴△PDK≌△QDA,
∴DK=AD=$\frac{1}{2}$(6-2t)=3-t,DH=AD•sin60°=$\frac{\sqrt{3}}{2}$(3-t),EQ=$\frac{1}{2}$BQ=$\frac{1}{2}$(6+2t)=3+t,
∴S=$\frac{1}{2}$•QE•DH=-$\frac{\sqrt{3}}{4}$t2+$\frac{9\sqrt{3}}{4}$.
②如图3中,当t>3时,作PK∥AB交AC于K,则△PCK是等边三角形.作DH⊥AB于H.
由△PDK≌△QDA,
∴DK=AD=$\frac{1}{2}$(2t-6)=t-3,DH=AD•sin60°=$\frac{\sqrt{3}}{2}$(t-3),EQ=$\frac{1}{2}$BQ=$\frac{1}{2}$(6+2t)=3+t,
∴S=$\frac{1}{2}$•QE•DH=$\frac{\sqrt{3}}{4}$t2-$\frac{9\sqrt{3}}{4}$.
综上所述,S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{4}{t}^{2}+\frac{9\sqrt{3}}{4}}&{(0<t≤3)}\\{\frac{\sqrt{3}}{4}{t}^{2}-\frac{9\sqrt{3}}{4}}&{(t>3)}\end{array}\right.$.
(3)①如图4中,当0≤t≤3时,作QK⊥OA于K.则AK=t,FQ=OK=6-t,
当PB=FQ时,四边形PBQF是平行四边形,
∴6-2t=6-t,解得t=0.
②当t>3时,由PB=QF时,2t-6=6-t,解得t=4,
③当点Q在y轴左侧时,由PB=QF可得,t-6=2t-6,解得t=0,此种情形不存在.
综上所述,当t=0或4s时,以P、B、F、Q为顶点的四边形为平行四边形.
点评 本题考查四边形综合题、坐标与图形的性质、菱形的性质、三角形的面积、全等三角形的判定和性质、平行四边形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,学会用方程的思想思考问题,属于中考压轴题.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
| 时间t/s | 0 | 10 | 20 | 30 |
| 油温w/℃ | 10 | 25 | 40 | 55 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=-2 | B. | x=$\frac{1}{2}$ | C. | x=-$\frac{1}{2}$ | D. | x=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:| LED灯泡 | 普通白炽灯泡 | |
| 进价(元) | 45 | 25 |
| 标价(元) | 60 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com