
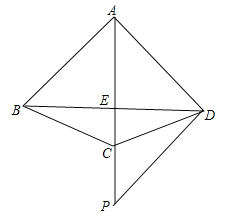
【题目】(2017山东省泰安市)如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)直接利用等腰三角形的性质结合互余的定义得出∠BDC=∠PDC;
(2)首先过点C作CM⊥PD于点M,进而得出△CPM∽△APD,求出EC的长即可得出答案.
试题解析:解:(1)∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90°.∵AC=AD,∴∠ACD=∠ADC,∴∠ADC+∠BDC=90°.∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC;
(2)过点C作CM⊥PD于点M,∵∠BDC=∠PDC,∴CE=CM,∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴![]() ,设CM=CE=x,∵CE:CP=2:3,∴PC=
,设CM=CE=x,∵CE:CP=2:3,∴PC=![]() x,∵AB=AD=AC=1,∴
x,∵AB=AD=AC=1,∴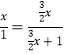 ,解得:x=
,解得:x=![]() ,故AE=1﹣
,故AE=1﹣![]() =
=![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种型号的节能灯共1000只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
(1)如果进货款恰好为37000元,那么可以购进甲型节能灯多少只?
(2)超市为庆祝元旦进行大促销活动,决定对乙型节能灯进行打折销售,要求全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于
的延长线于![]() ,且
,且![]() ,连接
,连接![]() .
.
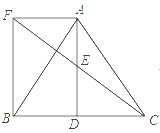
(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)若![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
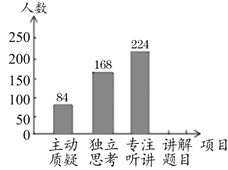
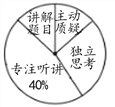
【题目】某地区教育部门为了解初中数学课堂中学生参与情况,并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价.检测小组随机抽查部分学校若干名学生,并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图(均不完整).请根据统计图中的信息解答下列问题:
(1)本次抽查的样本容量是 ;
(2)在扇形统计图中,“主动质疑”对应的圆心角为 度;
(3)将条形统计图补充完整;
(4)如果该地区初中学生共有60000名,那么在课堂中能“独立思考”的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小知识:如图,我们称两臂长度相等(即![]() )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角![]() ,则底角
,则底角![]() .
.
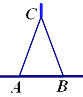
请运用上述知识解决问题:
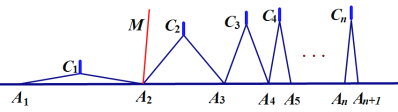
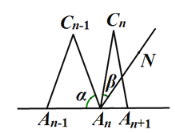
如图,![]() 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,…
,…
(1)、①由题意可得![]() = ;
= ;
②若![]() 平分
平分![]() ,则
,则![]() = ;
= ;
(2)、![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(3)、当![]() 时,设
时,设![]() 的度数为
的度数为![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 构成的角的度数为
构成的角的度数为![]() ,那么
,那么![]() 与
与![]() 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
查看答案和解析>>
科目:初中数学 来源: 题型:
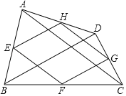
【题目】如图,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是四边形
分别是四边形![]() 边
边![]() 、
、![]() 、
、![]() 、
、![]() 的中点.则下列说法:①若
的中点.则下列说法:①若![]() ,则四边形
,则四边形![]() 为矩形;②若
为矩形;②若![]() ,则四边形
,则四边形![]() 为菱形;③若四边形
为菱形;③若四边形![]() 是平行四边形,则
是平行四边形,则![]() 与
与![]() 互相平分;④若四边形
互相平分;④若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 互相垂直且相等.其中正确的个数是( )
互相垂直且相等.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】喜迎新年,某社区超市第一次用5000元购进甲、乙两种商品,其中甲商品件数是品的件数的2倍,甲、乙两种商品的进价和售价如下表:
甲 | 乙 | |
进价(元/件) | 15 | 20 |
售价(元/件) | 30 | 30 |
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)能市第二次以第一次的进价又购进甲、乙两种商品,其中购进乙种商品的件数不变,购进甲种商品的件数是第一次购进甲种商品件数的2倍;乙商品按原价销售,甲商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多600元,求第二次甲种商品按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是反比例函数y=![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )

查看答案和解析>>
科目:初中数学 来源: 题型:
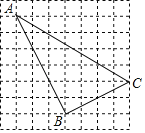
【题目】已知图中的每个方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC的顶点在格点上,称为格点三角形,请按要求完成下列各题
(1)填空:
AB= ,BC= ,AC= ;
(2)试判断△ABC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com