练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在学习概率的课堂上，老师提出问题：只有一张电影票，小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小明和小刚都公平的方案．
    甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．
    （1）甲同学的方案公平吗？请用列表或画树状图的方法说明；
    （2）乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？（只回答，不说明理由）

    【答案】
    （1）

    解：甲同学的方案不公平．理由如下：

    列表法，

    小明

    小刚

    2

    3

    4

    5

    2

    （2，3）

    （2，4）

    （2，5）

    3

    （3，2）

    （3，4）

    （3，5）

    4

    （4，2）

    （4，3）

    （4，5）

    5

    （5，2）

    （5，3）

    （5，4）

    所有可能出现的结果共有12种，其中抽出的牌面上的数字之和为奇数的有：8种，故小明获胜的概率为：，则小刚获胜的概率为：，

    故此游戏两人获胜的概率不相同，即他们的游戏规则不公平；


    （2）

    解：不公平．理由如下：

    小明

    小刚

    2

    3

    4

    2

    （2，3）

    （2，4）

    3

    （3，2）

    （3，4）

    4

    （4，2）

    （4，3）

    所有可能出现的结果共有6种，其中抽出的牌面上的数字之和为奇数的有：4种，故小明获胜的概率为：，则小刚获胜的概率为：，

    故此游戏两人获胜的概率不相同，即他们的游戏规则不公平．


    【解析】（1）依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率，比较即可．
    （2）解题思路同上．
    【考点精析】本题主要考查了列表法与树状图法的相关知识点，需要掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作等腰直角△ABC，使∠BAC=90°，取BC的中点P．当点B从点O向x轴正半轴移动到点M（2，0）时，则点P移动的路线长为 ．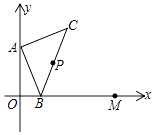

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某花木公司在20天内销售一批马蹄莲．其中，该公司的鲜花批发部日销售量y1（万朵）与时间x（x为整数，单位：天）部分对应值如下表所示．

    时间x（天）

    0

    4

    8

    12

    16

    20

    销量y1（万朵）

    0

    16

    24

    24

    16

    0

    另一部分鲜花在淘宝网销售，网上销售日销售量y2（万朵）与时间x（x为整数，单位：天） 关系如图所示．

    （1）请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律，写出y1与x的函数关系式及自变量x的取值范围；
    （2）观察马蹄莲网上销售量y2与时间x的变化规律，请你设想商家采用了何种销售策略使得销售量发生了变化，并写出销售量y2与x的函数关系式及自变量x的取值范围；
    （3）设该花木公司日销售总量为y万朵，写出y与时间x的函数关系式，并判断第几天日销售总量y最大，并求出此时最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校是乒乓球体育传统项目学校，为进一步推动该项目的开展，学校准备到体育用品店购买直拍球拍和横拍球拍若干副，并且每买一副球拍必须要买10个乒乓球，乒乓球的单价为2元/个，若购买20副直拍球拍和15副横拍球拍花费9000元；购买10副横拍球拍比购买5副直拍球拍多花费1600元．
    （1）求两种球拍每副各多少元？
    （2）若学校购买两种球拍共40副，且直拍球拍的数量不多于横拍球拍数量的3倍，请你给出一种费用最少的方案，并求出该方案所需费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（列方程（组）及不等式解应用题）
    春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．
    （1）求甲、乙两种商品每件的进价分别是多少元？
    （2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE交BD于G，交BC于H，下列结论：①∠DBE=∠F；②2∠BEF=∠BAF+∠C；③∠F=（∠BAC﹣∠C）；④∠BGH=∠ABE+∠C.

    其中正确的是（　　）

    A. ①②③ B. ①③④ C. ①②④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（　　）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题背景：
    如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
    小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE= CD，从而得出结论：AC+BC= CD．
    简单应用：

    （1）在图①中，若AC= ，BC=2 ，则CD= ．
    （2）如图③，AB是⊙O的直径，点C、D在⊙上， = ，若AB=13，BC=12，求CD的长．
    拓展规律：
    （3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）
    （4）如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE= AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB∥CD，∠B=90°，AB=AD=5，BC=4，M、N、E分别是AB、AD、CB上的点，AM=CE=1，AN=3，点P从点M出发，以每秒1个单位长度的速度沿折线MB﹣BE向点E运动，同时点Q从点N出发，以相同的速度沿折线ND﹣DC﹣CE向点E运动，当其中一个点到达后，另一个点也停止运动．设△APQ的面积为S，运动时间为t秒，则S与t函数关系的大致图象为（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案