
 在直角坐标系xOy中,?ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=-2x平行.
在直角坐标系xOy中,?ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=-2x平行.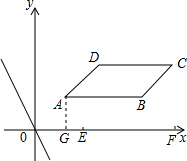
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 32-12 |
| 2 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
| A、950×1010km |
| B、95×1012km |
| C、9.5×1012km |
| D、0.95×1013km |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )
如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
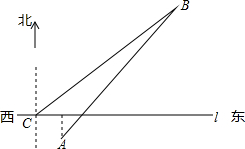 如图,港口A、B位于东西方向航道l的两侧,港口B在A的北偏东45°的方向,航道l上船C与港口B相距100海里,此时在C处测得港口B的方向北偏东55°,已知港口A到航道l距离为13海里,求两港口A、B之间的距离.(参考数据:sin35°≈0.57,cos35°≈0.82,
如图,港口A、B位于东西方向航道l的两侧,港口B在A的北偏东45°的方向,航道l上船C与港口B相距100海里,此时在C处测得港口B的方向北偏东55°,已知港口A到航道l距离为13海里,求两港口A、B之间的距离.(参考数据:sin35°≈0.57,cos35°≈0.82,| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
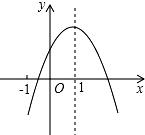 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有查看答案和解析>>
科目:初中数学 来源: 题型:
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ||
| 第一行 | 1 | 2 | 5 | 10 | 17 | … |
| 第二行 | 4 | 3 | 6 | 11 | 18 | … |
| 第三行 | 9 | 8 | 7 | 12 | 19 | … |
| 第四行 | 16 | 15 | 14 | 13 | 20 | … |
| 第五行 | 25 | 24 | 23 | 22 | 21 | … |
| … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com