
分析 先运用分母有理化求出x+$\frac{1}{x}$的值,再把所求的分式根据分式的基本性质进行变形,代入计算即可.
解答 解:∵x=$\frac{4-\sqrt{7}}{3}$,
∴x+$\frac{1}{x}$=$\frac{4-\sqrt{7}}{3}$+$\frac{3}{4-\sqrt{7}}$
=$\frac{4-\sqrt{7}}{3}$+$\frac{3(4+\sqrt{7})}{{4}^{2}-7}$
=$\frac{4-\sqrt{7}}{3}$+$\frac{4+\sqrt{7}}{3}$
=$\frac{8}{3}$
原式=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$
=$\frac{1}{{(x+\frac{1}{x})}^{2}-2+1}$
=$\frac{1}{{(\frac{8}{3})}^{2}-1}$
=$\frac{9}{55}$
点评 本题考查的是二次根式的化简求值,正确进行分母有理化和分式的变形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
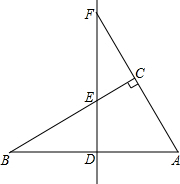 如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.
如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=0.2x+18.5(1≤x≤6) | B. | y=0.2x+18.7(1≤x≤6) | ||
| C. | y=0.2x+22(1≤x≤6) | D. | y=0.2x+22.2(1≤x≤6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
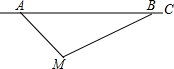 根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com