
【题目】如图,矩形ABCD中, AB=8,BC=4,P,Q分别是直线AB,AD上的两个动点,点![]() 在边
在边![]() 上,
上,![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 的最小值为( )
的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
作点C关于AB的对称点H,连接PH,EH,由已知求出CE=6,CH=8,由勾股定理得出EH=![]() =10,由SAS证得△PBC≌△PBH,得出CP=PH,PF+PC=PF+PH,当E、F、P、H四点共线时,PF+PH值最小,即可得出结果.
=10,由SAS证得△PBC≌△PBH,得出CP=PH,PF+PC=PF+PH,当E、F、P、H四点共线时,PF+PH值最小,即可得出结果.
解:作点C关于AB的对称点H,连接PH,EH,如图所示:
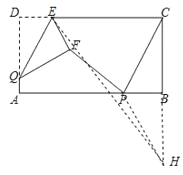
∵矩形ABCD中,AB=8,BC=4,DE=2,
∴CE=CDDE=ABDE=6,CH=2BC=8,
∴EH=![]() =10,
=10,
在△PBC和△PBH中,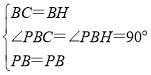 ,
,
∴△PBC≌△PBH(SAS),
∴CP=PH,
∴PF+PC=PF+PH,
∵EF=DE=2是定值,
∴当E、F、P、H四点共线时,PF+PH值最小,最小值=102=8,
∴PF+PD的最小值为8,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,四边形OABC的顶点A、C分别在x、y轴的正半抽上,点D是OA上的一点,OC=OD=4,OA=6,点B的坐标为(4,4).动点E从点C出发,以每秒![]() 个单位长度的速度沿线段CD向点D运动,过点E作BC的垂线EF交线段BC于点F,以线段EF为斜边向右作等腰直角△EFG.设点E的运动时间为t秒(0≤t≤4).
个单位长度的速度沿线段CD向点D运动,过点E作BC的垂线EF交线段BC于点F,以线段EF为斜边向右作等腰直角△EFG.设点E的运动时间为t秒(0≤t≤4).

(1)点G的坐标为( , )(用含t的代数式表示)
(2)连接OE、BG,当t为何值时,以O、C、E为顶点的三角形与△BFG相似?
(3)设点E从点C出发时,点E、F、G都与点C重合,点E在运动过程中,当△ABG 的面积为![]() 时,求点E运动的时间t的值,并直接写出点G从出发到此时所经过的路径长 (即线段AG的长).
时,求点E运动的时间t的值,并直接写出点G从出发到此时所经过的路径长 (即线段AG的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第10个图形中花盆的个数为( )

A. 110B. 120C. 132D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
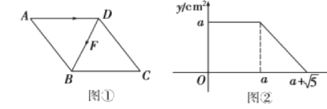
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)
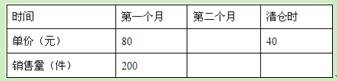
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
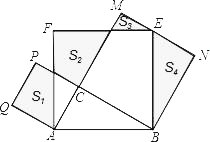
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
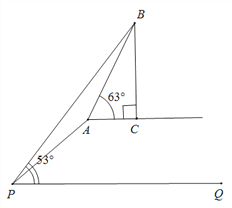
【题目】如图,坡度为1:2的斜坡AP的坡顶有一铁塔BC,在坡底P处测得塔顶B的仰角为53°,在沿斜坡前进![]() 米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
(参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈2,sin53°≈0.8,cos53°≈0.6,tan53°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com