
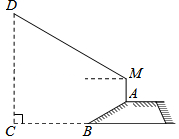
 如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.
如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.分析 (1)根据坡度的定义,利用三角函数即可求得坡角;
(2)由i的值求得大堤的高度h,点A到点B的水平距离a,从而求得MN的长度,由仰角求得DN的高度,从而由DN,AM,h求得高度CD.
解答 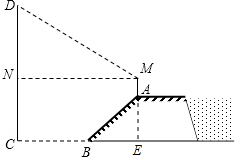 解:(1)过A点作AE垂直于CB的延长线于点E.
解:(1)过A点作AE垂直于CB的延长线于点E.
∵i=1:$\sqrt{3}$,
∴∠ABE=30°,
(2)∵AB=20m,
∴AE=$\frac{1}{2}$AB=$\frac{1}{2}$×20=10,
BE=ABcos30°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$,
∴CN=AE+AM=10+1.7=11.7,
MN=CB+BE=30+10$\sqrt{3}$,
∵∠NMD=30°,MN=30+10$\sqrt{3}$,
∴DN=MNtan30°=(30+10$\sqrt{3}$)×$\frac{\sqrt{3}}{3}$=10+10$\sqrt{3}$,
∴CD=CN+DN=11.7+10+10$\sqrt{3}$=21.7+10$\sqrt{3}$.
点评 本题考查了解直角三角形的应用-坡度坡角问题,由i的值求得堤坝的高AE和BE,求得MN,由仰角求得DN高度,进而求得总高度.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:填空题
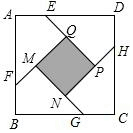 如图,在边长为a(a>2)的正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,则正方形MNPQ的面积为2.
如图,在边长为a(a>2)的正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,则正方形MNPQ的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
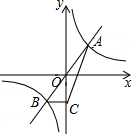 如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.
如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
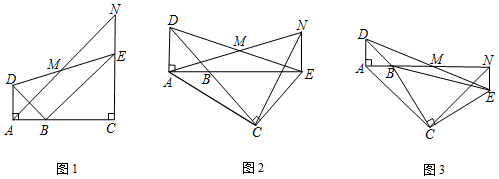
 请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.
请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com