
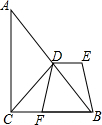
 已知:如图,△ABC中,∠ACB=90°,D为AB边中点,点F在BC边上,DE∥CF,且DE=CF.若DF=2,EB的长为2.
已知:如图,△ABC中,∠ACB=90°,D为AB边中点,点F在BC边上,DE∥CF,且DE=CF.若DF=2,EB的长为2. 分析 可通过构建全等三角形来证明,连接CD,那么CD就是直角三角形斜边上的中线,那么DC=DB,∠DCB=∠DBC,在三角形DCF和DEB中,已知的条件有DB=CD,ED=FC,只要再证得两组对应边的夹角相等即可得出全等的结论,由于ED、CF平行,那么∠EDB=∠DBC=∠DCB,这样就构成了两三角形全等的条件(SAS)就能得出EB=DF的结论了.
解答 解:∵∠ACB=90°,D是AB边的中点
∴DC=DB,∠DCB=∠DBC,
∵DE与CF平行且相等,
∴∠EDB=∠DBC=∠DCB,
在△AED和△CFD中
$\left\{\begin{array}{l}{DC=DB}\\{∠DCF=∠BDE}\\{CF=DE}\end{array}\right.$,
∴△AED≌△CFD
∴AE=DF=2,
故答案为:2
点评 此题考查简单的线段相等,可以通过构建全等三角形来证明.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.


科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,∠BAC=90°,AB=6,AC=8.
如图,已知△ABC,∠BAC=90°,AB=6,AC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
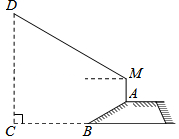 如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.
如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{\frac{x}{15}-15=y}\\{\frac{x}{12}+12=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{15}+15=y}\\{\frac{x}{12}-12=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{15}-\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{15}+\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某学员在广场上练习驾驶汽车,第一次向左拐弯15度行驶一段后,第二次向左拐弯13度,再次行驶一段后,那么第三次要向右拐弯28度,则行驶方向与原来行驶方向相同.
如图,某学员在广场上练习驾驶汽车,第一次向左拐弯15度行驶一段后,第二次向左拐弯13度,再次行驶一段后,那么第三次要向右拐弯28度,则行驶方向与原来行驶方向相同.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com