
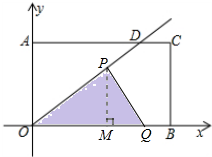
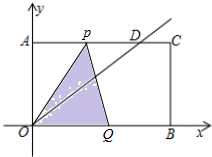
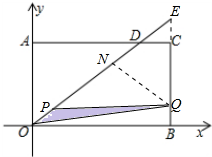
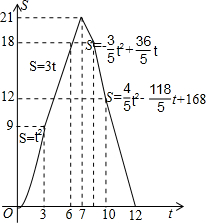
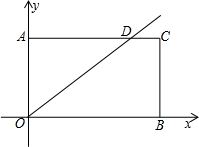
 x(x≥0)交线段AC于点D,点P从O点出发,以每秒2个单位长度的速度沿O→A→D→O的路线匀速运动;与此同时,点Q从O点出发,以每秒1个单位长度的速度沿O→B→C的路线匀速运动,当其中一点到达终点时,另一点也停止运动.设运动时间为t秒,△POQ的面积为S.
x(x≥0)交线段AC于点D,点P从O点出发,以每秒2个单位长度的速度沿O→A→D→O的路线匀速运动;与此同时,点Q从O点出发,以每秒1个单位长度的速度沿O→B→C的路线匀速运动,当其中一点到达终点时,另一点也停止运动.设运动时间为t秒,△POQ的面积为S.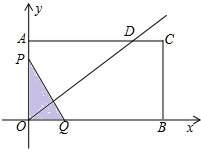
 (备用图)
(备用图) (24-2t),
(24-2t),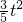 +
+ t
t +
+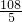
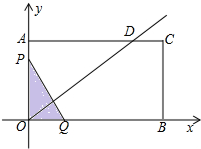
 ,BE=
,BE= ,
,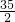 -t,NQ=
-t,NQ= (
(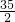 -t),
-t), (12-t)(35-2t)
(12-t)(35-2t)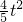 -
-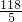 t+168
t+168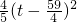 -
-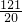
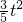 +
+ t=18,t=6+
t=18,t=6+ ,t=6-
,t=6- <7(舍).
<7(舍). ,
, ,
, (24-2t)=
(24-2t)= ,
, .
.
 x上,∴x=8,即AD=8,利用勾股定理可求得OD=10.
x上,∴x=8,即AD=8,利用勾股定理可求得OD=10.

科目:初中数学 来源: 题型:
| 3 | 4 |
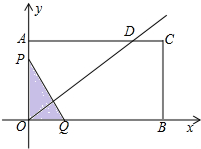
 (备用图)
(备用图)查看答案和解析>>
科目:初中数学 来源: 题型:
 (2007•郑州模拟)如图,矩形AOBC的两边OC、OA分别位于x轴、y轴上,点B的坐标为(-
(2007•郑州模拟)如图,矩形AOBC的两边OC、OA分别位于x轴、y轴上,点B的坐标为(-| 5 |
| 5 |
| 2 |
| x |
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源:2012年湖南省中考数学模拟试卷(一)(解析版) 题型:解答题
 的图象经过C,求双曲线和直线AB的解析式.
的图象经过C,求双曲线和直线AB的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com