
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.

【答案】(1)证明见解析;(2)5.
【解析】
(1)直接利用旋转的性质可得AP=AQ,∠PAQ=60°,然后根据“SAS”证明△BAP≌△CAQ,结合全等三角形的性质得出答案;
(2)由△APQ是等边三角形可得AP=PQ=3,∠AQP=60°,由全等的性质可得∠AQC =∠APB=150°,从而可求∠PQC=90°,然后根据勾股定理求PC的长即可.
直接利用等边三角形的性质结合勾股定理即可得出答案.
(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中
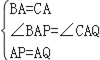 ,
,
∴△BAP≌△CAQ(SAS),
∴PB=QC;
(2)解:∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
∴PC=![]() =
=![]() =5.
=5.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点C为线段OB的中点,D为线段OA上一点.连结AC、BD交于点P.
(问题引入)(1)如图1,若点P为AC的中点,求![]() 的值.
的值.
温馨提示:过点C作CE∥AO交BD于点E.
(探索研究)(2)如图2,点D为OA上的任意一点(不与点A、O重合),求证:![]() .
.
(问题解决)(3)如图2,若AO=BO,AO⊥BO,![]() ,求tan∠BPC的值.
,求tan∠BPC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为一边向上作等边三角形
为一边向上作等边三角形![]() ,点
,点![]() 在
在![]() 垂直平分线上,且
垂直平分线上,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
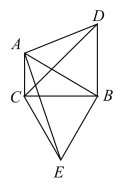
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)求证:![]() ;
;
(3)填空:
①若![]() ,
,![]() 相交于点
相交于点![]() ,则
,则![]() 的度数为______.
的度数为______.
②在射线![]() 上有一动点
上有一动点![]() ,若
,若![]() 为等腰三角形,则
为等腰三角形,则![]() 的度数为______.
的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防疾病,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量![]() (mg)与燃烧时间
(mg)与燃烧时间![]() (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后, ![]() 与
与![]() 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时![]() 与
与![]() 的函数关系式.(2)求药物燃烧后
的函数关系式.(2)求药物燃烧后![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
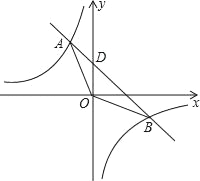
【题目】如图,反比例函数y=﹣![]() 与一次函数y=﹣x+2的图象交于A、B两点.
与一次函数y=﹣x+2的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,直接写出x为何值时,一次函数值大于反比例函数?
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com