
| A. | x<-$\frac{1}{2}$ | B. | x<2 | C. | x>-$\frac{1}{2}$ | D. | x>2 |
分析 首先判断出A在第二象限,再根据第二象限内点的坐标特点可得$\left\{\begin{array}{l}{2x+1<0①}\\{x-2<0②}\end{array}\right.$,再解不等式组即可.
解答 解:由题意得:$\left\{\begin{array}{l}{2x+1<0①}\\{x-2<0②}\end{array}\right.$,
由①得:x<-$\frac{1}{2}$,
由②得:x<2,
不等式组的解集为x$<-\frac{1}{2}$,
故选:A.
点评 此题主要考查了解一元一次不等式组,以及关于x轴对称点的坐标特点,关键是掌握关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )| A. | $\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元) | 0 | 100 | 200 | 300 | 400 |
| y(亩) | 600 | 1000 | 1400 | 1800 | 2200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
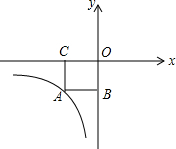 如图,正方形ABOC的边长是2,反比例函数y=$\frac{k}{x}$(x≠0)图象经过点A,则k的值是( )
如图,正方形ABOC的边长是2,反比例函数y=$\frac{k}{x}$(x≠0)图象经过点A,则k的值是( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 640人 | B. | 480人 | C. | 400人 | D. | 40人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com