
【题目】如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:
![]()
(1)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动 个单位;
(2)若移动A、B、C三点中的两个点,使三个点表示的数相同,移动方法有 种,其中移动所走的距离和最小的是 个单位;
(3)若在原点处有一只小青蛙,一步跳1个单位长.小青蛙第1次先向左跳1步,第2次再向右跳3步,然后第3次再向左跳5步,第4次再向右跳7步,…,按此规律继续跳下去,那么跳第100次时,应跳 步,落脚点表示的数是 ;
(4)若有两只小青蛙A、B,它们在数轴上的点表示的数分别为整数x、y,且|x﹣2|+|y+3|=2,求两只小青蛙A、B之间的距离.
【答案】(1)3或7;(2)3,7;(3)199,100;(4)3或5或7
【解析】试题分析:(1)由AB=2,结合数轴即可得出点C向左移动的距离;
(2)分为三种:移动B、C;移动A、C;移动A、B.然后计算每种情况移动所走的距离和即可;
(3)根据规律发现,所跳步数是奇数列,写出表达式,然后把n=100代入进行计算即可求解,根据向左跳是负数,向右跳是正数,列出算式,然后两个数一组,计算后再求和即可,当跳了n次时,分n是偶数与n是奇数两种情况讨论求解.
(4)根据题意, |x﹣2|与|x+3|都是整数.分三种情况进行分类讨论.
试题解析:解:(1)有数轴可知:A.B两点的距离为2,B点、C点表示的数分别为:﹣2、3,所以当C、B两点的距离与A、B两点的距离相等时,需将点C向左移动3个单位或7个单位,故答案为:3或7;
(2)有3种方法:①移动B、C,把点B向左移动2个单位长度,把C向左移动7个单位长度,移动距离之和为:2+7=9;
②移动A、C,把点A向右移动2个单位长度,把C向左移动5个单位长度,移动距离之和为:2+5=7;
③移动B、A,把点A向右移动7个单位长度,把B向左右移动5个单位长度,移动距离之和为:7+5=12.
所以移动所走的距离和最小的是7个单位,故答案为:3,7;
(3)∵第1次跳1步,第2次跳3步,第3次跳5步,第4次跳7步,…
∴第n次跳(2n﹣1)步,当n=100时,2×100﹣1=200﹣1=199,此时,所表示的数是:﹣1+3﹣5+7﹣…﹣197+199=(﹣1+3)+(﹣5+7)+…+(﹣197+199)=2×![]() =100;
=100;
(4)根据题意, |x﹣2|与|x+3|都是整数.分三种情况进行分类讨论:
①|x﹣2|=0,|y+3|=2,所以|x﹣y|=3或7;
②|x﹣2|=1,|y+3|=1.所以|x﹣y|=3或5或7;
③|x﹣2|=2,|y+3|=0.所以|x﹣y|=3或7;
故两青蛙之间的距离是3或5或7.


科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )
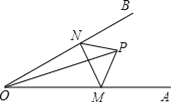
A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山西省第20题)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg~5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司手机有两类收费标准,A类收费标准如下:不管通话时间多长,少,每部手机每月必须缴月租费12元,另外,通话费按0.2元/min计。B类收费标准如下:没有月租费,但通话费按0.25元/min计。
(1)分别写出A、B两类每月应缴费用y(元)与通话时间x(min)之间的关系式;
(2)如果手机用户预算每月交55元的话费,那么该用户选择哪类收费方式合算?
(3)每月通话多长时间,按A、B两类收费标准缴费,所缴话费相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com