
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
【答案】解:(1)∵点A(1,4)在![]() 的图象上,∴
的图象上,∴![]() =1×4=4。
=1×4=4。
∴反比例函数的表达式为![]()
∵点B在![]() 的图象上,∴
的图象上,∴![]() 。∴点B(-2,-2)。
。∴点B(-2,-2)。
又∵点A、B在一次函数![]() 的图象上,
的图象上,
∴![]() ,解得
,解得![]() 。
。
∴一次函数的表达式为![]() 。
。
(2)由图象可知,当 0<![]() <1时,
<1时,![]() >
>![]() 成立
成立
(3)∵点C与点A关于![]() 轴对称,∴C(1,-4)。
轴对称,∴C(1,-4)。
过点B作BD⊥AC,垂足为D,则D(1,-5)。

∴△ABC的高BD=1![]() =3,底为AC=4
=3,底为AC=4![]() =8。
=8。
∴S△ABC=![]() AC·BD=
AC·BD=![]() ×8×3=12。
×8×3=12。
【解析】
(1)根据点A的坐标求出反比例函数的解析式为![]() ,再求出B的坐标是(-2,-2),利用待定系数法求一次函数的解析式。
,再求出B的坐标是(-2,-2),利用待定系数法求一次函数的解析式。
(2)当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出当![]() >0时,一次函数的值小于反比例函数的值x的取值范围或0<x<1。
>0时,一次函数的值小于反比例函数的值x的取值范围或0<x<1。
(3)根据坐标与线段的转换可得出:AC、BD的长,然后根据三角形的面积公式即可求出答案。


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)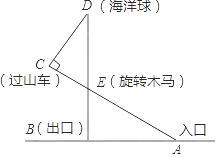
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠DAB的平分线交CD于E点,且DE=5,EC=8.

(1)求□ABCD的周长;
(2)连结AC,若AC=12,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,把
,把![]() 的直角三角板
的直角三角板![]() 的直角顶点
的直角顶点![]() 放在直线
放在直线![]() 上.将直角三角板
上.将直角三角板![]() 在平面内绕点
在平面内绕点![]() 任意转动,若转动的过程中,直线
任意转动,若转动的过程中,直线![]() 与直线
与直线![]() 的夹角为60°,则
的夹角为60°,则![]() 的度数为___.
的度数为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)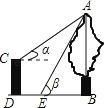
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】禁渔期间,我渔政船在A处发现正北方向B处有一艘可以船只,测得A、B两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,![]() 与
与![]() 、
、![]() 、
、![]() 的数量关系为____.
的数量关系为____.
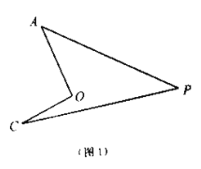
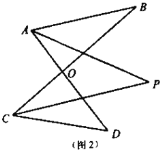
(2)如图(2),已知![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
由(1)结论得:![]()
所以![]() 即
即![]()
因为![]()
![]()
所以![]()
所以![]() .
.
解决问题:
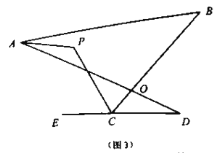
(1)如图(3),直线![]() 平分
平分![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 与
与![]() 、
、![]() 的数量关系是______;
的数量关系是______;
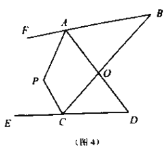
(2)如图(4),直线![]() 平分
平分![]() 的外角
的外角![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 与
与![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 ![]() 可化为3x=6.
可化为3x=6.
D.方程 ![]() 系数化为1,得x=﹣1
系数化为1,得x=﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com