
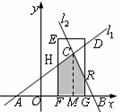
如图,已知直线 与直线
与直线 相交于点
相交于点 分别交
分别交 轴
轴 两点.矩形
两点.矩形 的顶点
的顶点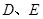 分别在直线
分别在直线 上,顶点
上,顶点 都在
都在 轴上,且点
轴上,且点 与点
与点 重合.
重合.

(1)求 的面积;
的面积;
(2)求矩形 的边
的边 与
与 的长;
的长;
(3)若矩形 从原点出发,沿
从原点出发,沿 轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形
轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形 与
与 重叠部分的面积为
重叠部分的面积为 ,求
,求 关于的函数关系式.
关于的函数关系式.
(1)36;(2)4,8;(3)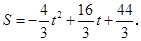
【解析】
试题分析:(1)先分别求得两条直线与x轴的交点坐标,再求得两条直线的交点坐标,最后根据三角形的面积公式求解即可;
由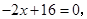 得
得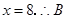 点坐标为
点坐标为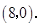
(2)根据矩形的性质即可求的 点的坐标,再根据点
点的坐标,再根据点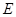 在
在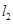 上即可求得
上即可求得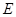 点的坐标,即得结果;
点的坐标,即得结果;
(3)当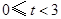 时,如图,矩形
时,如图,矩形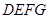 与
与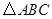 重叠部分为五边形
重叠部分为五边形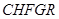 (
(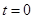 时,为四边形
时,为四边形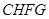 ).过
).过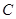 作
作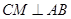 于
于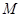 ,证得
,证得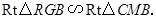 再根据相似三角形的性质及三角形的面积公式求解即可.
再根据相似三角形的性质及三角形的面积公式求解即可.
(1)由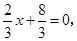 得
得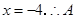 点坐标为
点坐标为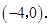
由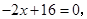 得
得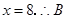 点坐标为
点坐标为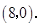
∴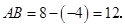
由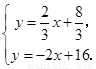 解得
解得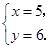
∴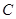 点的坐标为
点的坐标为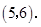
∴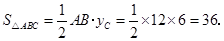
(2)∵点 在
在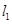 上且
上且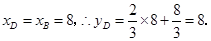
∴ 点坐标为
点坐标为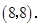
又∵点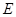 在
在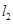 上且
上且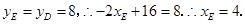
∴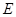 点坐标为
点坐标为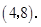
∴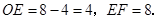
(3)当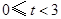 时,如图,矩形
时,如图,矩形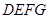 与
与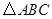 重叠部分为五边形
重叠部分为五边形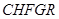 (
(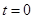 时,为四边形
时,为四边形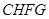 ).过
).过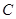 作
作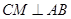 于
于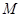 ,
,
则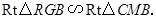
∴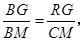 即
即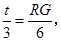 ∴
∴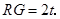
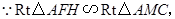
∴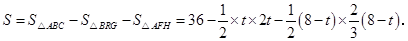
即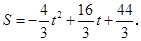
考点:函数的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题

 时,求直线a′的函数解析式;
时,求直线a′的函数解析式;查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线![]() 与直线
与直线![]() 相交于点
相交于点![]() 分别交
分别交![]() 轴
轴![]() 两点.矩形
两点.矩形![]() 的顶点
的顶点![]() 分别在直线
分别在直线![]() 上,顶点
上,顶点![]() 都在
都在![]() 轴上,且点
轴上,且点![]() 与点
与点![]() 重合.
重合.

(1)求![]() 的面积;
的面积;
(2)求矩形![]() 的边
的边![]() 与
与![]() 的长;
的长;
(3)若矩形![]() 从原点出发,沿
从原点出发,沿![]() 轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形
轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于的函数关系式.
关于的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2013届广东省珠海市香洲区中考二模数学试卷(带解析) 题型:解答题
如图,已知直线 与直线
与直线 相交于点
相交于点 分别交
分别交 轴
轴 两点.矩形
两点.矩形 的顶点
的顶点 分别在直线
分别在直线 上,顶点
上,顶点 都在
都在 轴上,且点
轴上,且点 与点
与点 重合.
重合.
(1)求 的面积;
的面积;
(2)求矩形 的边
的边 与
与 的长;
的长;
(3)若矩形 从原点出发,沿
从原点出发,沿 轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形
轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形 与
与 重叠部分的面积为
重叠部分的面积为 ,求
,求 关于的函数关系式.
关于的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2011年4月浙江省某区中考数学二模试卷(解析版) 题型:解答题
 时,求直线a′的函数解析式;
时,求直线a′的函数解析式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com