解:(1)对于y=3x+6,可求B(0,6).
∴OB=6,
∵C(8,0),
∴OC=8.
∴BC=

=10.
∴sin∠BCA=
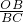
=
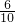
=

.
(2)由y=3x+6可求A(-2,0),
∴AC=BC=10.
∴S
△ABC=

AC×OB=

×10×6=30.
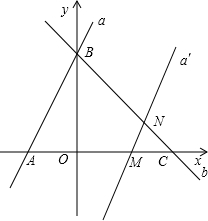
∵a′∥a,
∴△MCN∽△ABC.
∴
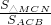
=(
)
2,
∵S
△MCN=

,
∴
=

.
∴MC=5.
∴M(3,0).
设a′为y=3x+b,代入M(3,0)得b=-9.
∴直线a′解析式为y=3x-9.
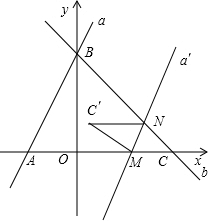
(3)由(2)可知,当m=5时,点C′正好在AB上.
∴当5≤m≤10时,点C′在△ABC内,如图所示.
此时,重叠部分面积S=S
△MC′N=S
△MCN=(
)
2•S
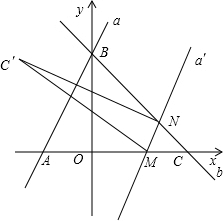
△ABC=30×(
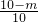
)
2=

(10-m)
2,
当0≤m≤5时,点C
′在△AB外内,如图所示.
∵AC=BC=10,
∴△ABC是等腰三角形,易知△AEM,
△BFN,△MCN都是与△ABC相似的等腰三角形.
∴S
△AEM=(
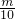
)
2•S
△ABC=S
△BFN,S
△MCN=(
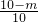
)
2•S
△ABC,
∴重叠部分面积S=30-(
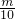
)
2×30×2-(
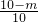
)
2×30,
=6m-

m
2综上可知:
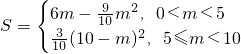
显然,在5≤m<10范围内,当m=5时,S最大=

;而根据二次函数性质,在0<m<5范围内,当m=

时,S最大=10.
所以,在0<m<10时,当m=

时,S最大=10.
易知MCNC
′是菱形,所以当S最大时,
四边形MCNC
′的周长=4×(10-m)=4×(10-

)=
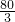
.
分析:(1)根据直线的性质,求出B、C的坐标,在直角三角形BOC中,根据正弦函数的定义即可求出sin∠BCA的值;
(2)求出S
△ABC,根据△MCN∽△ABC,利用相似三角形的面积比等于相似比的平方,求出M点的坐标,利用待定系数法求直线a′的函数解析式即可;
(3)根据翻折不变性,可知S
△MC′N=S
△MCN,利用(2)的结论即可得到其面积表达式,然后即可根据m的取值范围推出三角形面积的最大值.
点评:此题考查了二次函数的图象和直线及三角形面积的关系,综合性很强,不仅要熟悉函数的图象和性质,更要熟悉翻折变换和相似三角形的性质,难度较大,须认真读题.


 时,求直线a′的函数解析式;
时,求直线a′的函数解析式;
 =10.
=10.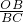 =
=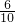 =
= .
. AC×OB=
AC×OB= ×10×6=30.
×10×6=30.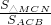 =(
=(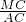 )2,
)2, ,
,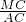 =
= .
.
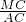 )2•S△ABC=30×(
)2•S△ABC=30×(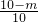 )2=
)2= (10-m)2,
(10-m)2,
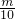 )2•S△ABC=S△BFN,S△MCN=(
)2•S△ABC=S△BFN,S△MCN=(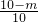 )2•S△ABC,
)2•S△ABC,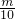 )2×30×2-(
)2×30×2-(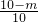 )2×30,
)2×30, m2
m2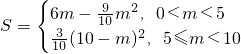
 ;而根据二次函数性质,在0<m<5范围内,当m=
;而根据二次函数性质,在0<m<5范围内,当m= 时,S最大=10.
时,S最大=10. 时,S最大=10.
时,S最大=10. )=
)=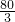 .
.

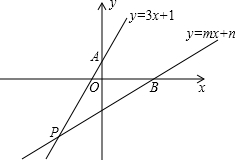 如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题: