
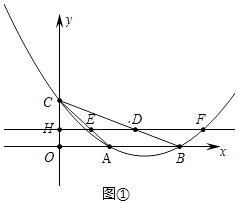
【题目】如图①,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=﹣x+2经过A、C两点,且AB=2.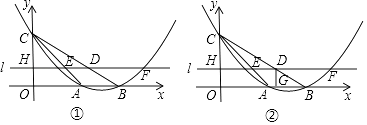
(1)求抛物线的解析式;
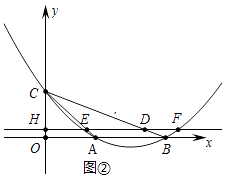
(2)若直线l平行于x轴,直线l从点C出发以每秒1个单位长度的速度沿y轴负半轴方向向点O运动,到点O停止,且分别交线段AC、线段BC、抛物线、y轴于点E、D、F(点F在对称轴的右侧)、H,当点D是线段EF的三等分点时,求t的值;
(3)如图②,在直线l运动的过程中,过点D作x轴的垂线交x轴于点G,四边形OHDG与△AOC重叠部分的面积为S,求S与t的函数关系式.
【答案】
(1)
解:∵直线y=﹣x+2与x轴、y轴的交点为A(2,0),C(0,2),AB=2,
∴B(4,0),
把A(2,0)、B(4,0)、C(0,2)代入y=ax2+bx+c中,
得 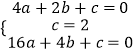 ,解得
,解得 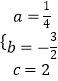 ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:∵OA=OC=2,
∴△AOC是等腰直角三角形,
∵直线l∥x轴,
∴△HEC是等腰直角三角形,
∵OA=AB=2,
∴HE=DE,
① 如图①中,当DF=2DE时,点F坐标(4t,2﹣t),
∴2﹣t= ![]() ×(4t)2﹣
×(4t)2﹣ ![]() ×4t+2,
×4t+2,
∴t= ![]() 或0(舍弃),
或0(舍弃),
②如图2中,当DE=2DF时,点F坐标( ![]() t,2﹣t),
t,2﹣t),
∴2﹣t= ![]() ×(
×( ![]() t)2﹣
t)2﹣ ![]() ×
× ![]() t+2,
t+2,
∴t= ![]() 或0(舍弃),
或0(舍弃),
综上所述,当点D是线段EF的三等分点时,t的值为 ![]() s或
s或 ![]() s
s
(3)
解:①如图③当0<t≤1时,重叠部分是五边形EHOGK,
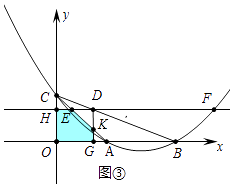
S=S矩形OHDG﹣S△DEK=2t(2﹣t)﹣ ![]() t2=﹣
t2=﹣ ![]() t2+4t,
t2+4t,
②如图④中,当1<t<2时,重叠部分是四边形OHEA,
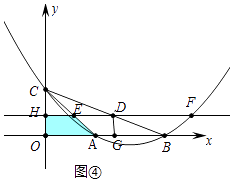
S= ![]() (t+2)(2﹣t)=﹣
(t+2)(2﹣t)=﹣ ![]() t2+2,
t2+2,
综上所述,S=  .
.
【解析】(1)求出A、B、C三点坐标,代入抛物线的解析式,解方程组即可.(2)分两种情形①如图①中,当DF=2DE时,点F坐标(4t,2﹣t),②如图2中,当DE=2DF时,点F坐标( ![]() t,2﹣t),想办法列出方程解决问题.(3)分两种情形①如图③当0<t≤1时,重叠部分是五边形EHOGK,②如图④中,当1<t<2时,重叠部分是四边形OHEA,分别计算即可.
t,2﹣t),想办法列出方程解决问题.(3)分两种情形①如图③当0<t≤1时,重叠部分是五边形EHOGK,②如图④中,当1<t<2时,重叠部分是四边形OHEA,分别计算即可.
【考点精析】通过灵活运用求根公式和相似三角形的性质,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( ) 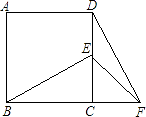
A.10°
B.15°
C.20°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,平移抛物线y=x2﹣2x+3,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A,O,B为顶点的三角形是等腰直角三角形,求平移后的抛物线的解析式. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1, ![]() )在反比例函数y=
)在反比例函数y= ![]() (x>0)的图象上,连接OA,将线段OA绕点O沿顺时针方向旋转30°,得到线段OB.
(x>0)的图象上,连接OA,将线段OA绕点O沿顺时针方向旋转30°,得到线段OB.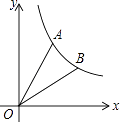
(1)求反比例函数的解析式;
(2)填空:
①点B的坐标是;
②判断点B是否在反比例函数的图象上?答;
③设直线AB的解析式为y=ax+b,则不等式ax+b﹣ ![]() <0的解集是 .
<0的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( ) 
A.![]()
B.![]()
C.![]()
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象交于M,N两点.
(k≠0)的图象交于M,N两点. 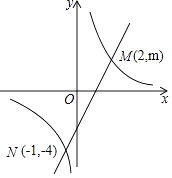
(1)求反比例函数与一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=∠ADC=90°,BD⊥AC,垂足为P. 
(1)请作出Rt△ABC的外接圆⊙O;(保留作图痕迹,不写作法)
(2)点D在⊙O上吗?说明理由;
(3)试说明:AC平分∠BAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com