
����Ŀ����ͼ�ı���ABCD�����Σ��ҡ�ABC=60����ABE�ǵȱ������Σ�MΪ�Խ���BD������B�㣩������һ�㣬��BM�Ƶ�B��ʱ����ת60��õ�BN������EN��AM��CM�������������������ȷ���ǣ� ��
��������ABCD�ı߳�Ϊ1����AM+CM����Сֵ1��
�ڡ�AMB�ա�ENB��
��S�ı���AMBE=S�ı���ADCM��
������AN����AN��BE��
�ݵ�AM+BM+CM����СֵΪ2 ![]() ʱ������ABCD�ı߳�Ϊ2��
ʱ������ABCD�ı߳�Ϊ2��
A.�٢ڢ�
B.�ڢܢ�
C.�٢ڢ�
D.�ڢۢ�
���𰸡�C
���������⣺������AC����BD�ڵ�O��
���ı���ABCD�����Σ�
��AB=BC��BD��AC��AO=BO
���A����C����ֱ��BD�Գƣ�
��M����O���غ�ʱAM+CM��ֵ��СΪAC��ֵ
�ߡ�ABC=60��
���ABC�ǵȱ������Σ�
��AB=AC��
��AB=1��
��AC=1��
��AM+CM��ֵ��СΪ1���ʱ�����ȷ��
�ڡߡ�ABE�ǵȱ������Σ�
��BA=BE����ABE=60�㣮
�ߡ�MBN=60�㣬
���MBN����ABN=��ABE����ABN��
����MBA=��NBE��
�֡�MB=NB��
���AMB�ա�ENB��SAS�����ʱ�����ȷ��
�ۡ�S��ABE+S��ABM=S�ı���AMBE
S��ACD+S��AMC=S�ı���ADCM �� ��S��AMB��S��AMC ��
��S��ABE+S��ABM��S��ACD+S��AMC ��
��S�ı���AMBE��S�ı���ADCM �� �ʱ��𰸴���
�ܼ���AN��BE����AE=AB��
��AN��BE�Ĵ�ֱƽ���ߣ�
��EN=BN=BM=MN��
��M����O���غϣ�
������û��ȷ��M����O���غϣ��ʱ��𰸴���
����ͼ������MN���ɣ�1��֪����AMB�ա�ENB��
��AM=EN��
�ߡ�MBN=60�㣬MB=NB��
���BMN�ǵȱ������Σ�
��BM=MN��
��AM+BM+CM=EN+MN+CM����10�֣�
���ݡ�����֮���߶���̡�����EN+MN+CM=EC���
�൱M��λ��BD��CE�Ľ��㴦ʱ��AM+BM+CM��ֵ��С��������EC�ij���
��E����EF��BC��CB���ӳ�����F��
���EBF=180�㩁120��=60�㣬�����εı߳�Ϊx��
��BF= ![]() x��EF=
x��EF= ![]() x����Rt��EFC��
x����Rt��EFC��
��EF2+FC2=EC2 ��
�� ![]() +
+ ![]() =
= ![]() �����x=2���ʱ�����ȷ��
�����x=2���ʱ�����ȷ��
������������ȷ�Ĵ��ǣ��٢ڢݣ�
��ѡC��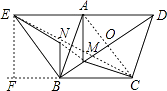
��1������AC�����ݡ�����֮���߶���̡����ɵã���M������BD���е�ʱ��AM+CM��ֵ��С����2���������MB=NB����ABN=30�㣬���ԡ�EBN=30�㣬����֤����AMB�ա�ENB����3������AC�����Եõ�S��ABE=S��ADC �� S��AMB��S��AMC �� �Ӷ����Եó����ۣ���4������AN��BE�����ݵ��������ε����ʼ���ֱƽ���ߵ����ʵó�EN=BN���Ӷ��ó����ۣ���5�����ݡ�����֮���߶���̡�����M��λ��BD��CE�Ľ��㴦ʱ��AM+BM+CM��ֵ��С��������EC�ij�������ͼ���������ߣ���E����EF��BC��CB���ӳ�����F�������������EBF=60�㣬�����εı߳�Ϊx����Rt��EFC�У����ݹ��ɶ���������εı߳���


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д� ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CD�ǡ�O��һ���ң���CD��AB�ڵ�E��CD=4 ![]() ��AE=2�����O�İ뾶Ϊ ��
��AE=2�����O�İ뾶Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ˣ�2������֯��һ�ξ����ʶ��������ס������Ӹ�10�˵ı����ɼ����±���10���ƣ���
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
��1���ӳɼ�����λ�����֣��Ҷӳɼ����������֣�
��2�������Ҷӵ�ƽ���ɼ��ͷ��
��3����֪�ӳɼ��ķ�����1.4��2 �� ��ɼ���Ϊ��������ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AC��BD�ཻ�ڵ�O��EΪAB���е㣬DE��AB�� 
��1�����ABC�Ķ�����
��2����� ![]() ����DE�ij���
����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������6�·ݣ�����ij��ũ�ջ���֦30�֣��㽶13�֣��ּƻ����üס������ֻ�����10��������ˮ��ȫ���������ڣ���֪���ֻ�����װ��֦4�ֺ��㽶1�֣����ֻ�����װ��֦�㽶��2�֣� 
��1���ù�ũ���żס������ֻ���ʱ�м��ַ��������������Ƴ�����
��2�������ֻ���ÿ��Ҫ�������2000Ԫ�����ֻ���ÿ��Ҫ�������1300Ԫ����ù�ũӦѡ�����ַ���ʹ�˷����٣������˷��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ��Ƴ���������ͳ��ͼ�� 
����������Ϣ�����������������£�
ƽ���ɼ�/�� | ��λ��/�� | ����/�� | ���� | |
�� | a | 7 | 7 | 1.2 |
�� | 7 | b | 8 | c |
��1��д��������a��b��c��ֵ��
��2���ֱ����ñ��е��ĸ�ͳ��������Ҫ������������Ա�����ѵ���ɼ�����ѡ������һ������������ΪӦѡ������Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
��1����ͼ1������AF��CE����֤�ı���AFCEΪ���Σ�����AF�ij��� 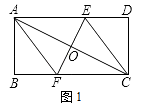
��2����ͼ2������P��Q�ֱ��A��C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У�
����֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
������P��Q���˶�·�̷ֱ�Ϊa��b����λ��cm��ab��0������֪A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���a��b�����������ϵʽ��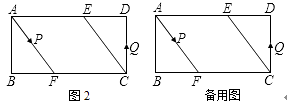
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC���DEF��Ϊ�ȱ������Σ�OΪBC��EF���е㣬��AD��BE��ֵΪ�� �� 
A.![]() ��1
��1
B.![]() ��1
��1
C.5��3
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��������ABCD�ı�BC�ӳ�����һ�㣬����DE��������B��BF��DE������ΪF��BF�ֱ�AC��H����BC��G�� 
��1����֤��BG=DE��
��2������GΪCD���е㣬�� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com