
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G. 
(1)求证:BG=DE;
(2)若点G为CD的中点,求 ![]() 的值.
的值.
【答案】
(1)解:∵BF⊥DE,
∴∠GFD=90°,
∵∠BCG=90°,∠BGC=∠DGF,
∴∠CBG=∠CDE,
在△BCG与△DCE中,
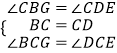
∴△BCG≌△DCE(ASA),
∴BG=DE,
(2)解:设CG=1,
∵G为CD的中点,
∴GD=CG=1,
由(1)可知:△BCG≌△DCE(ASA),
∴CG=CE=1,
∴由勾股定理可知:DE=BG= ![]() ,
,
∵sin∠CDE= ![]() =
= ![]() ,
,
∴GF= ![]() ,
,
∵AB∥CG,
∴△ABH∽△CGH,
∴ ![]() =
= ![]() ,
,
∴BH= ![]() ,GH=
,GH= ![]() ,
,
∴ ![]() =
= ![]()
【解析】(1)由于BF⊥DE,所以∠GFD=90°,从而可知∠CBG=∠CDE,根据全等三角形的判定即可证明△BCG≌△DCE,从而可知BG=DE;(2)设CG=1,从而知CG=CE=1,由勾股定理可知:DE=BG= ![]() ,由易证△ABH∽△CGH,所以
,由易证△ABH∽△CGH,所以 ![]() ,从而可求出HG的长度,进而求出
,从而可求出HG的长度,进而求出 ![]() 的值.
的值.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图四边形ABCD是菱形,且∠ABC=60,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为2 ![]() 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
A.①②③
B.②④⑤
C.①②⑤
D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图题:
(1)如图,将△ABC绕点O顺时针旋转180°后得到△A1B1C1 . 请你画出旋转后的△A1B1C1; 
(2)请你画出下面“蒙古包”的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( ) 
A.12
B.15
C.16
D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE. 
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2cm的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是m2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行使路程y(千米)与行驶时间x(分钟)之间的函数图象如图所示. 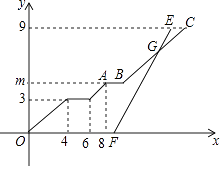
(1)求点A的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE. 
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com