
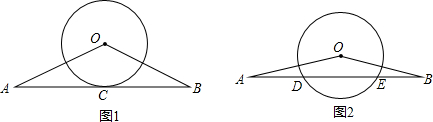
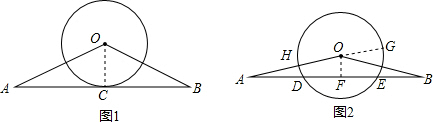
 解:(1)连接OC,
解:(1)连接OC,| AC2+OC2 |
| AO2-AF2 |
| 153-144 |
| 9 |
| OF |
| AF |
| 3 |
| 12 |
| 1 |
| 4 |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:044
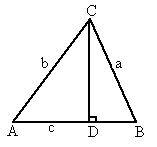
(2007,新疆维吾尔自治区、新疆生产建设兵团,23)在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c如图所示,过C作CD⊥AB于D,则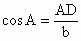 ,即AD=bcosA
,即AD=bcosA
∴BD=c-AD=c-bcosA
在Rt△ADC和Rt△BDC中有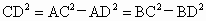 ∴
∴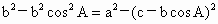
整理得: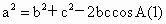
同理可得: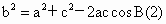
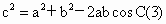
这个结论就是著名的余弦定理.在以上三个等式中有六个元素a、b,c,∠A、∠B、∠C,若已知其中的任意三个元素,可求出其余的另外三个元素.
如:在锐角△ABC中,已知∠A=60°,b=3,c=6
则由(1)式可得: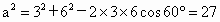
∴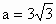 ,∠B,∠C则可由式子(2)、(3)分别求出,在此略.
,∠B,∠C则可由式子(2)、(3)分别求出,在此略.
根据以上阅读理解,请你试着解决如下问题:
已知锐角△ABC的三边a、b、c分别是7、8、9,求∠A、∠B、∠C的度数(保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年内蒙古包头市中考数学试卷(课标版)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com