
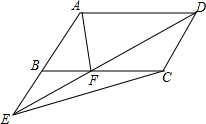
 如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF.
如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF. 分析 分别过点E、D作EG⊥BC、DH⊥BC,交直线BC于G、H,根据平行四边形的性质得出BE∥CD,那么△BEF∽△CDF,利用相似三角形对应高的比等于相似比得到BF•DH=CF•EG,即可解决问题.
解答 证明: 如图,分别过点E、D作EG⊥BC、DH⊥BC,交直线BC于G、H.
如图,分别过点E、D作EG⊥BC、DH⊥BC,交直线BC于G、H.
∵四边形ABCD是平行四边形,
∴BE∥CD,
∴△BEF∽△CDF,
∴$\frac{BF}{CF}$=$\frac{EG}{DH}$,即BF•DH=CF•EG,
∵S△ABF=$\frac{1}{2}$BF•DH,S△EFC=$\frac{1}{2}$CF•EG,
∴S△ABF=S△CEF.
点评 该题主要考查了平行四边形的性质、相似三角形的判定及性质,三角形的面积等知识;解题的关键是正确作出辅助线


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
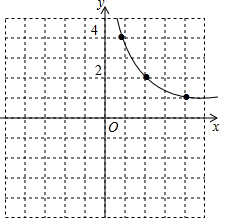 已知反比例函数y=$\frac{k}{x}$,图中已经画出了此函数图象的其中一支,请根据图中所给信息,把这个反比例函数图象的另一支补充完整.
已知反比例函数y=$\frac{k}{x}$,图中已经画出了此函数图象的其中一支,请根据图中所给信息,把这个反比例函数图象的另一支补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
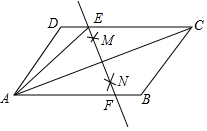 在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.
在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中:
如图所示,在△ABC中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF. 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
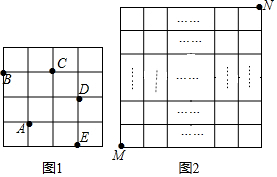
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com