
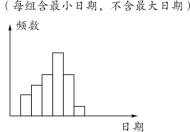
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图(如图所示).已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)哪组上交的作品数量最少?有多少件?
(4)第二组上交的作品数量是多少件?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
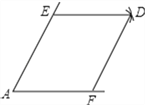
【题目】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A,∠B,∠C的对应边分别是a,b,c,则满足下列条件但不是直角三角形的是( )
A. ∠A=∠B-∠C B. ∠A:∠B:∠C=1:3:4 C. a:b:c=1:![]() :3 D.
:3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,
连接EF,则EF=BE+DF,试说明理由.

(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°
∴点F、D、G共线
根据 ,易证△AFG≌ ,进而得EF=BE+DF.
(2)联想拓展
如图2,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的数量关系,并写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,顺德区政府招商办准备引荐本区的龙头企业与 “一带一路”沿线国家和地区合作.负责人要为这些企业制作一批宣传材料,联系了甲、乙两家设计公司,甲公司提出:每份材料收费20元,另加设计费3000元;乙公司提出:每份材料收费30元,不收设计费.在其他条件完全相同的情况下,区招商负责人选择哪间公司比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0( ) 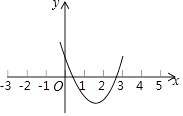
A.没有实根
B.只有一个实根
C.有两个实根,且一根为正,一根为负
D.有两个实根,且一根小于1,一根大于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|=6+7;|6-7|=7-6;|7-6|=7-6;|-6-7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=_________;
(2)|![]() |=____________;
|=____________;
(3)|![]() |=__________;
|=__________;
(4)用合理的方法计算:|![]() |+|
|+|![]() |-
|-![]() ×|-
×|-![]() |+
|+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com