
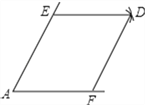
【题目】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】学校为数学竞赛准备了若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为竞赛的奖品.若购买2支钢笔和3本笔记本需62元,购买5支钢笔和1本笔记本需90元.
(1)购买一支钢笔和一本笔记本各需多少钱?
(2)若学校准备购买钢笔和笔记本共80件奖品,并且购买的费用不超过1100元,则学校最多可以购买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年暑期临近,学生们也可轻松逛逛商场,选择自己心仪的衣服![]() 安岳上府街一服装店老板打算不错失这一良机,计划购进甲、乙两种T恤
安岳上府街一服装店老板打算不错失这一良机,计划购进甲、乙两种T恤![]() 已知购进甲T恤2件和乙T恤3件共需310元;购进甲T恤1件和乙T恤2件共需190元
已知购进甲T恤2件和乙T恤3件共需310元;购进甲T恤1件和乙T恤2件共需190元
![]() 求甲、乙两种T恤每件的进价分别是多少元?
求甲、乙两种T恤每件的进价分别是多少元?
![]() 为满足市场需求,服装店需购进甲、乙两种T恤共100件,要求购买两种T恤的总费用不超过6540元,并且购买甲T恤的数量应小于购买甲乙两种T恤总数量的
为满足市场需求,服装店需购进甲、乙两种T恤共100件,要求购买两种T恤的总费用不超过6540元,并且购买甲T恤的数量应小于购买甲乙两种T恤总数量的![]() ,请你通过计算,确定服装店购买甲乙两种T恤的购买方案.
,请你通过计算,确定服装店购买甲乙两种T恤的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,AD=21cm,BC=16cm,DC=12cm,动点P从D开始沿DA向A以2cm/s的速度运动;动点Q从点C开始向B以1cm/s的速度运动.P、Q分别从点D、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.
(1)如图1,当t为何值时,四边形APQB是平行四边形
(2)△BPQ是等腰三角形,则有三种情况:BP=BQ,PB=PQ,QP=QB.
①当BP=BQ时,此情况不成立;
②当PB=PQ时,如图2,作PM⊥BC,则BM=_________________,QM=_________________,(用含t的式子表示),得到t=________________.
③当QP=QB时,请求出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.
(1)求菱形ABCD的面积;(2)求∠CHA的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图:
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;

(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
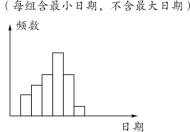
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图(如图所示).已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)哪组上交的作品数量最少?有多少件?
(4)第二组上交的作品数量是多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com