设x1，x2是关于x的方程x2+px+q=0的两根，x1+1，x2+1是关于x的方程x2+qx+p=0的两根，则p，q的值分别等于（ ）
A．1，-3
B．1，3
C．-1，-3
D．-1，3
【答案】
分析：已知两方程的根，由根与系数的关系得：x
1+x
2=-p，x
1•x
2=q；x
1+1+x
2+1=-q，（x
1+1）（x
2+1）=p，
即x
1+x
2+x
1•x
2+1=p，将x
1+x
2=-p，x
1•x
2=q分别代入，消去x
1、x
2，解关于p、q的二元一次方程组可求解．
解答：解：由根与系数的关系可知：x
1+x
2=-p，x
1•x
2=q；
x
1+1+x
2+1=-q，（x
1+1）（x
2+1）=p，即x
1+x
2+x
1•x
2+1=p．
将x
1+x
2=-p，x
1•x
2=q代入整理，得
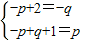
解得
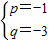
．故选C
点评：本题主要考查一元二次方程根与系数的关系．
阅读快车系列答案
