
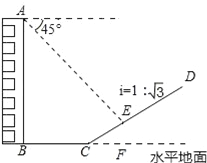
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
【答案】楼房AB的高为(35+10![]() )米.
)米.
【解析】试题分析:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,根据CE=20米,坡度为i=1: ![]() ,分别求出EF、CF的长度,在Rt△AEH中求出AH,继而可得楼房AB的高.
,分别求出EF、CF的长度,在Rt△AEH中求出AH,继而可得楼房AB的高.
试题解析:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i=![]() =
=![]() =tan∠ECF,
=tan∠ECF,
∴∠ECF=30°,
∴EF=![]() CE=10米,CF=10
CE=10米,CF=10![]() 米,
米,
∴BH=EF=10米,HE=BF=BC+CF=(25+10![]() )米,
)米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(25+10![]() )米,
)米,
∴AB=AH+HB=(35+10![]() )米.
)米.
答:楼房AB的高为(35+10![]() )米.
)米.


科目:初中数学 来源: 题型:
【题目】某年级组织学生参加夏令营,分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况.请你根据图中的信息回答下列问题:![]()
![]()
报名人数分布直方图 报名人数扇形统计图
(1)求该年级报名参加本次活动的总人数;
(2)求该年级报名参加乙组的人数,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,那么,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点 ![]() 分别在正方形
分别在正方形 ![]() 的边
的边 ![]() 上,
上, ![]() ,连接
,连接 ![]() ,则
,则 ![]() ,试说明理由.
,试说明理由.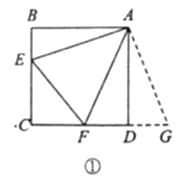
(1)思路梳理
因为 ![]() ,所以把
,所以把 ![]() 绕点
绕点 ![]() 逆时针旋转90°至
逆时针旋转90°至 ![]() ,可使
,可使 ![]() 与
与 ![]() 重合.因为
重合.因为 ![]() ,所以
,所以 ![]() ,点
,点 ![]() 共线.
共线.
根据 , 易证 ![]() , 得
, 得 ![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 分别在边
分别在边 ![]() 上,
上, ![]() .若
.若 ![]() 都不是直角,则当
都不是直角,则当 ![]() 与
与 ![]() 满足等量关系时,
满足等量关系时, ![]() 仍然成立,请证明.
仍然成立,请证明.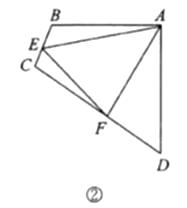
(3)联想拓展
如图③,在 ![]() 中,
中, ![]() ,点
,点 ![]() 均在边
均在边 ![]() 上,且
上,且 ![]() .猜想
.猜想 ![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.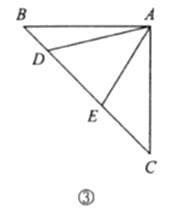
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )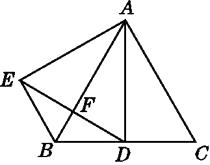
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次新冠病毒防疫知识竞赛有25道题,评委会决定:答对一道题得4分,答错或不答一题扣1分,在这次知识竞赛中,小明被评为优秀(85分或85分以上),那么小明至少答对了__________道题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A. ![]() B.
B. ![]() C. 1 D. 0
C. 1 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com