【题目】如图，△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D．
（1）若△BCD的周长为8，求BC的长；
（2）若∠A=40°，求∠DBC的度数．
【答案】（1）3cm；（2）30°.
【解析】试题分析：(1)、根据线段垂直平分线定理得出AD=BD，根据BC+CD+BD=8cm求出AC+BC=8cm，把AC的长代入求出即可；(2)、已知∠A=40°，AB=AC可得∠ABC=∠ACB，再由线段垂直平分线的性质可求出∠ABC=∠A，易求∠DBC．
试题解析：(1)、∵D在AB垂直平分线上， ∴AD=BD， ∵△BCD的周长为8cm，
∴BC+CD+BD=8cm， ∴AD+DC+BC=8cm， ∴AC+BC=8cm， ∵AB=AC=5cm，
∴BC=8cm﹣5cm=3cm；
(2)、∵∠A=40°，AB=AC， ∴∠ABC=∠ACB=70°， 又∵DE垂直平分AB， ∴DB=AD
∴∠ABD=∠A=40°， ∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°．
科目：初中数学 来源： 题型：
【题目】如图所示，已知∠AOB=α，在射线OA、OB上分别取点OA1=OB1，连结A1B1，在B1A1、B1B上分别取点A2、B2，使B1B2=B1A2，连结A2B2…按此规律下去，记∠A2B1 B2=θ1，∠A3B2B3=θ2，…，∠An+1Bn Bn+1=θn，则θ2016﹣θ2015的值为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的材料：
如图1，在数轴上A点衰示的数为a，B点表示的数为b，则点A到点B的距离记为AB．线段AB的长可以用右边的数减去左边的数表示，即AB﹣b﹣a．
请用上面的知识解答下面的问题：
如图2，一个点从数轴上的原点开始，先向左移动1cm到达A点，再向左移动2cm到达B点，然后向右移动7cm到达C点，用1个单位长度表示1cm．
（1）请你在数轴上表示出A．B．C三点的位置：
（2）点C到点人的距离CA= cm；若数轴上有一点D，且AD=4，则点D表示的数为 ；
（3）若将点A向右移动xcm，则移动后的点表示的数为 ；（用代数式表示）
（4）若点B以每秒2cm的速度向左移动，同时A．C点分别以每秒1cm、4cm的速度向右移动．设移动时间为t秒，
试探索：CA﹣AB的值是否会随着t的变化而改变？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
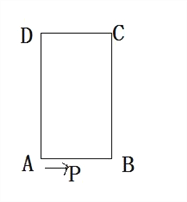
【题目】如图，长方形ABCD中，AB=4cm，BC=6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A—B—C—D回到点A，设点P的运动时间为t秒。
（1）当t=3秒时，求△ABP的面积；
（2）当t为何值时，点P与点A的距离为5cm？
（3）当t为何值时（2＜t＜5），以线段AD、CP、AP的长度为三角形是直角三角形，且AP是斜边。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点C是线段AB的中点，点D是线段AC的中点，点E是线段BC的中点．
（1）若线段DE=11cm，求线段AB的长．
（2）若线段CE=4cm，求线段DB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售一种西装和领带，西装每套定价200元，领带每条定价40元.国庆节期间商场决定开展促销活动，活动期间向客户提供两种优惠方案：
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套，领带x
.
（1）若该客户按方案一购买，需付款多少元（用含x的式子表示）？若该客户按方案二购买，需付款多少元（用含x的式子表示）？
（2）若
，通过计算说明此时按哪种方案购买较为合算；
（3）当
时，你能给出一种更为省钱的购买方法吗？试写出你的购买方法和所需费用.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠A与∠B的平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列事件中，必然发生的是（ ）
A. 某射击运动射击一次，命中靶心
B. 掷一次骰子，向上的一面是6点
C. 通常情况下，水加热到100℃时沸腾
D. 抛一枚硬币，落地后正面朝上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com