
分析 (1)两个连续奇数的平方差等于8的倍数,由此得出第n个等式为(2n+1)2-(2n-1)2=8n,由此解决问题即可;
(2)利用(1)中的规律求得答案即可.
解答 解:(1)∵32-12=8=8×1;
52-32=16=8×2:
72-52=24=8×3;
92-72=32=8×4
…
∴第n个等式为(2n+1)2-(2n-1)2=8n;
(2)把(1)中的两边的式子相加得
8×(1+2+3+4+…+n)=(2n+1)2-12
1+2+3+4+…+n=$\frac{2n(2n+2)}{8}$=$\frac{n(n+1)}{2}$.
点评 此题考查数字的变化规律,根据数字的特点,得出运算的规律,利用规律解决问题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
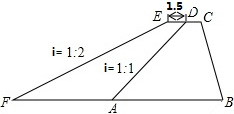 如图,为了防洪,某地区计划将长为1000m的一堤面加宽1.5m,背水坡坡度由原来1:1改为1:2,已知原背水坡坡长AD=8.0m,求完成这一工程所需的土方.(精确到1m3,$\sqrt{2}$≈1.414)
如图,为了防洪,某地区计划将长为1000m的一堤面加宽1.5m,背水坡坡度由原来1:1改为1:2,已知原背水坡坡长AD=8.0m,求完成这一工程所需的土方.(精确到1m3,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 角的两边画的越长,这个角就越大 | |
| B. | 角的大小与角的两边所画的长短无关 | |
| C. | 角的大小和它们的度数的大小是不一致的 | |
| D. | 角大,它的度数不一定大 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com