
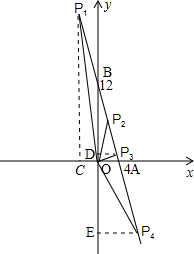
 解:(1)∵直线y=kx+b与直线y=-3x平行且过点(3,3),
解:(1)∵直线y=kx+b与直线y=-3x平行且过点(3,3),| 10 |
| AB |
| AP1 |
| BO |
| CP1 |
| AB |
| BP1 |
| AO |
| CO |
4
| ||
4
|
| 12 |
| CP1 |
4
| ||
| 12 |
| 4 |
| CO |
| 18 |
| 5 |
| 10 |
6
| ||
| 5 |
6
| ||
| 5 |
| 18 |
| 5 |
| 10 |
| BD |
| BO |
| BP3 |
| BA |
| P3D |
| AO |
| BD |
| 12 |
| 12 | ||
4
|
| P3D |
| 4 |
18
| ||
| 5 |
9
| ||
| 10 |
18
| ||
| 5 |
9
| ||
| 10 |
18
| ||
| 5 |
6
| ||
| 5 |
| 18 |
| 5 |
| 10 |
9
| ||
| 10 |
18
| ||
| 5 |


科目:初中数学 来源: 题型:
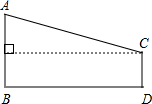 如图,磐石某风景名胜为了方便游人参观,从主峰A处假设了一条揽车线路到另一山峰C处,若主峰A的高度AB=120米,山峰C的高度CD=20米,两山峰的底部BD相距900米,求缆车线路AC的长.
如图,磐石某风景名胜为了方便游人参观,从主峰A处假设了一条揽车线路到另一山峰C处,若主峰A的高度AB=120米,山峰C的高度CD=20米,两山峰的底部BD相距900米,求缆车线路AC的长.查看答案和解析>>
科目:初中数学 来源: 题型:
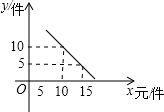 某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销量y(件)与零售价x(元/件)均成如图的一次函数关系.
某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销量y(件)与零售价x(元/件)均成如图的一次函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com