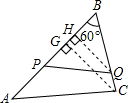
解:(1)分别过C,Q作CG⊥AB,QH⊥AB于G,H,
∵BC=16,∠B=60°,
∴CG=BC•sin60°=

,
又∵AB=24,
∴S
△ABC=

AB•CG=96

,
又∵AP=4t,CQ=2t,
∴BP=24-4t,BQ=16-2t(0<t<8),
∴QH=BQ•sin60°=(8-t)

,
∴S
△PBQ=

BP•QH=

×(24-4t)×(8-t)

,
又∵S
△PBQ=

S
△ABC,
∴

×(24-4t)×(8-t)

=

×96

,
∴t
2-14t+24=0,
∴t
1=2,t
2=12(舍去),
∴当t为2秒时,△PBQ的面积是△ABC的面积的一半.
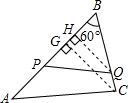
(2)当t=2时,HQ=6

,BQ=12,BP=16,
∴BH=

BQ=6,PH=16-6=10,
又∵在Rt△PQH中,PQ
2=HQ
2+PH
2,
∴PQ=
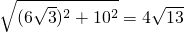
.
分析:(1)作辅助线,分别过C,Q作CG⊥AB,QH⊥AB于G,H,在Rt△BCG中,已知BC,∠B的值,可求出CG的值,代入S
△ABC进行求解,根据AP和CQ的值,可将BP,BQ的值表示出来,在Rt△BQH中,根据三角函数可将QH的值求出,代入S
△PBQ=

BP•QH,再根据S
△PBQ与S
△ABC的关系,从而可求出时间t;
(2)当t=2时,可将BP,BQ的值求出,在Rt△BHQ中,根据三角函数可将BH,HQ的值求出,进而可将PH的值求出,在Rt△PQH中,根据勾股定理可求出PQ的值,当t=12时,同理可将PQ的值求出.
点评:考查综合应用解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力,在求P、Q两点之间的距离时应分两种情况讨论.

 发,沿线段CB向点B运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,运动时间为t秒,求:
发,沿线段CB向点B运动,如果点P的速度是4cm/s,点Q的速度是2cm/s,它们同时出发,运动时间为t秒,求: 解:(1)分别过C,Q作CG⊥AB,QH⊥AB于G,H,
解:(1)分别过C,Q作CG⊥AB,QH⊥AB于G,H, ,
, AB•CG=96
AB•CG=96 ,
, ,
, BP•QH=
BP•QH= ×(24-4t)×(8-t)
×(24-4t)×(8-t) ,
, S△ABC,
S△ABC, ×(24-4t)×(8-t)
×(24-4t)×(8-t) =
= ×96
×96 ,
, (2)当t=2时,HQ=6
(2)当t=2时,HQ=6 ,BQ=12,BP=16,
,BQ=12,BP=16, BQ=6,PH=16-6=10,
BQ=6,PH=16-6=10,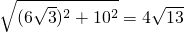 .
. BP•QH,再根据S△PBQ与S△ABC的关系,从而可求出时间t;
BP•QH,再根据S△PBQ与S△ABC的关系,从而可求出时间t;

 灵星计算小达人系列答案
灵星计算小达人系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为