
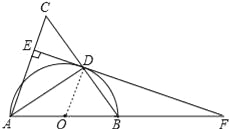
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)求证:△FDB∽△FAD;
(3)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
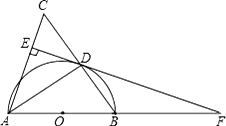
【答案】解:(1)证明:如图,连接OD,
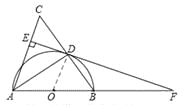
∵AB为⊙O的直径,∴∠ADB=90°。
∴AD⊥BC。
∵AB=AC,∴AD平分BC,即DB=DC。
∵OA=OB,∴OD为△ABC的中位线。
∴OD∥AC。
∵DE⊥AC,∴OD⊥DE。
∵OD是⊙O的半径,∴EF是⊙O的切线。
(2)∵∠DAC=∠DAB,∴∠ADE=∠ABD。
∴在Rt△ADB中, ![]() 。
。
∵AB=10,∴AD=8,
∵在Rt△ADE中, ![]() ,∴
,∴![]() 。
。
∵OD∥AE,∴△FDO∽△FEA。
∴![]() ,即
,即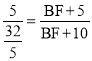 ,解得
,解得![]() 。
。
【解析】试题分析:(1)连接OD,AB为⊙0的直径得∠ADB=90°,由AB=AC,根据等腰三角形性质得AD平分BC,即DB=DC,则OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,则OD⊥DE,然后根据切线的判定方法即可得到结论;
(2)利用两角对应相等的两三角形相似进行证明即可.
(3)由∠DAC=∠DAB,根据等角的余角相等得∠ADE=∠ABD,在Rt△ADB中,利用解直角三角形的方法可计算出AD=8,在Rt△ADE中可计算出AE=![]() ,然后由OD∥AE,得△FDO∽△FEA,再利用相似比可计算出BF.
,然后由OD∥AE,得△FDO∽△FEA,再利用相似比可计算出BF.
试题解析:(1)证明:连接OD,如图,
∵AB为⊙0的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分BC,即DB=DC,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴EF是⊙0的切线;
(2)证明:∵EF是⊙O的切线,
∴∠ODB+∠BDF=90°,
∵OD=OB,
∴∠OBD=∠ODB,
∴∠OBD+∠BDF=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠OBD=90°,
∴∠DAB=∠BDF,
∵∠BFD=∠DFA,
∴△FDB∽△FAD;
(3)∵∠DAC=∠DAB,
∴∠ADE=∠ABD,
在Rt△ADB中,sin∠ADE=sin∠ABD=![]() ,而AB=10,
,而AB=10,
∴AD=8,
在Rt△ADE中,sin∠ADE=![]() ,
,
∴AE=![]() ,
,
∵OD∥AE,
∴△FDO∽△FEA,
∴![]() ,
,
即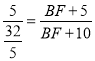 ,
,
∴BF=![]() .
.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( ) 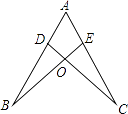
A.∠B=∠C
B.BE=CD
C.BD=CE
D.AD=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年广东省政府工作报告中指出:我省大力实施乡村振兴战略,加快解决农业农村突出问题,“三农”工作取得新成效,省财政自2018年起三年投入75亿元支持粤东粤西粤北省级现代农业产业园建设.用科学记数法表示75亿为( )
A. 7.5×108B. 0.75×1010C. 75×108D. 7.5×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中, 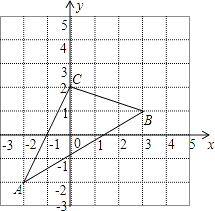
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家游泳中心﹣﹣“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260 000平方米,将260 000用科学记数法表示应为( )
A.0.26×106
B.26×104
C.2.6×106
D.2.6×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com