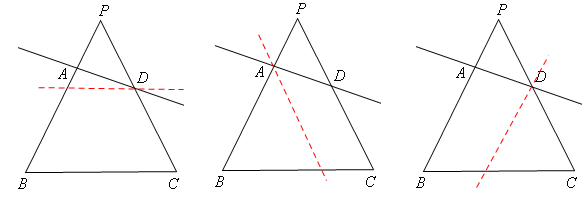
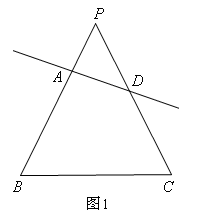
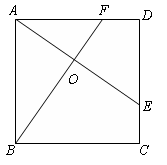
解:(1)作图如下:(画出一种示意图即可,答案不唯一)
(2)证明:∵AE∥DC,∴∠AEB=∠C。
又∵AB∥DE,∴∠B=∠DEC。∴△ABE∽△DCE。
∴
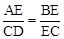
。
又∵∠B=∠C,∴∠B=∠AEB。∴AB=AE。
∴
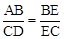
。
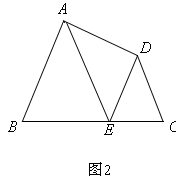
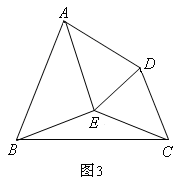
(3)如图,过点E分别作EF⊥AB,EG⊥AD,AH⊥CD,垂足分别 是F,G,H,
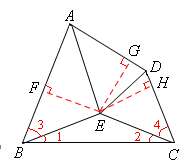
∵AE平分∠BAD,∴EF=EG。
又∵ED平分∠BAD,∴EG=EH。∴EF= EH。
又∵EB=EC,∴Rt△BEF≌Rt△CEF(HL)。∠3=∠4。
又∵EB=EC,∴∠1=∠2。
∴∠1+∠3=∠2+∠4,即∠ABC=∠DCB。
∴四边形ABCD是 “准等腰梯形”。
当点E不在四边形ABCD内部时,有两种情况:
当点E在四边形ABCD的边BC上时,四边形ABCD仍为 “准等腰梯形”;
当点E在四边形ABCD的外部时,四边形ABCD仍为 “准等腰梯形”。
(1)根据平行线的性质,过点D作BC的平行线或点D作PB的平行线或点A作PC的平行线,都能线将四边形ABCD分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形,作法不唯一。
(2)易证△ABE∽△DCE,可得
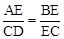
,由∠B=∠C可证得AB=AE,从而得证。
(3)过点E分别作EF⊥AB,EG⊥AD,AH⊥CD,垂足分别 是F,G,H,根据角平分线上的点到角的两边距离相等的性质,可得EF=EG= EH,从而可由HL证得 Rt△BEF≌Rt△CEF,从而∠3=∠4;由EB=EC,得∠1=∠2,根据等量加等量和相等,得∠ABC=∠DCB,即四边形ABCD是 “准等腰梯形”。
分点E在四边形ABCD的边BC上和点E在四边形ABCD的外部两种情况研究。

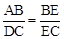

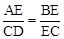 。
。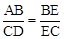 。
。
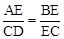 ,由∠B=∠C可证得AB=AE,从而得证。
,由∠B=∠C可证得AB=AE,从而得证。

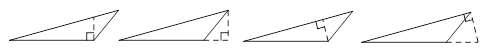
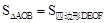 中正确的有
中正确的有



