
【题目】已知函数f(x)=ex﹣asinx﹣1,a∈R.
(1)若a=1,求f(x)在x=0处的切线方程;
(2)若f(x)≥0在区间[0,1)恒成立,求a的取值范围.
【答案】
(1)解: a=1时,f(x)=ex﹣sinx﹣1,f′(x)=ex﹣cosx,
∴f′(0)=e0﹣cos0=0,且f(0)=e0﹣sin0﹣1=0,
∴f(x)在x=0处的切线方程为:y=0
(2)f(x)≥0在区间[0,1)恒成立asinx≤ex﹣1在区间[0,1)恒成立.
①当x=0时,a∈R,
②当x∈(0,1)时,原不等式等价于a ![]() ,
,
令h(x)= ![]() ,x∈(0,1)
,x∈(0,1)
h′(x)= ![]() ,
,
令G(x)=exsinx﹣excosx+cosx,(x∈(0,1))
G′(x)=(2ex﹣1)sinx≥0,在x∈(0,1)恒成立.
∴G(x)=exsinx﹣excosx+cosx,(x∈(0,1))单调递增,而G(0)=0.
故G(x)≥0在(0,1)上恒成立,∴h′(x)≥在(0,1)上恒成立.
h(x)在(0,1)上递增,
x→0时,sinx→0,ex﹣1→0,
由洛必达法则得 ![]() =
= ![]() =
= ![]() ,
,
即a≤1,
综上,a的取值范围为(﹣∞,1]
【解析】(1)利用导数的几何意义,求出切线的斜率、切点,由点斜式写出方程.(2)f(x)≥0在区间[0,1)恒成立asinx≤ex﹣1在区间[0,1)恒成立.①当x=0时,a∈R,②当x∈(0,1)时,原不等式等价于a ![]() , 令h(x)=
, 令h(x)= ![]() ,x∈(0,1),利用导数求出h(x)在(0,1)上递增,由洛必达法则得
,x∈(0,1),利用导数求出h(x)在(0,1)上递增,由洛必达法则得 ![]() =
= ![]() =
= ![]() ,即可求得a的取值范围
,即可求得a的取值范围
【考点精析】关于本题考查的函数的最大(小)值与导数,需要了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=38°,在OB上有一点E , 从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )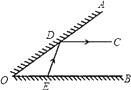
A.76°
B.52°
C.45°
D.38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时, |
当21≤x≤30时, |
(1)请计算第15天该商品单价为多少元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( ) 
A.与平面A1DE垂直的直线必与直线BM垂直
B.异面直线BM与A1E所成角是定值
C.一定存在某个位置,使DE⊥MO
D.三棱锥A1﹣ADE外接球半径与棱AD的长之比为定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(a∈R)与函数 ![]() 有公共切线. (Ⅰ)求a的取值范围;
有公共切线. (Ⅰ)求a的取值范围;
(Ⅱ)若不等式xf(x)+e>2﹣a对于x>0的一切值恒成立,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD. 
(Ⅰ)证明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD= ![]() ,DC=SD=2,点M在侧棱SC上,∠ABM=60°.
,DC=SD=2,点M在侧棱SC上,∠ABM=60°. 
(Ⅰ)证明:M是侧棱SC的中点;
(Ⅱ)求二面角S﹣AM﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com