
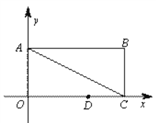
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,����OABC�ı�OA��y�����������,OC��x����������ϣ�OA=1,OC=2,��D�ڱ�OC����OD=1.25��
��1����ֱ��AC�Ľ���ʽ��
��2����y�����Ƿ���ڵ�P,ֱ��PD����ζԽ���AC���ڵ�M,ʹ�á�DMCΪ���������Σ�������,ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3��������y=-x2��������ƽ��,����ʹ��ƽ�ƺ�������߹���D�͵�E����E��y���������ϣ�,�ҡ�ODE��DE�۵����O���ڱ�AB��O/����
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�����������������£������ţ���֪��߿����иͣ���֪�䳤�̣���ţ��ͱ��ſ�����4�ߣ����ţ��ͱ��Ÿ߳���2�ߣ�б�ţ������ŶԽ��߳�ǡ����ȣ����Ÿߡ����ͶԽ��ߵij����Ƕ��٣����ŶԽ��ߵij�Ϊx�ߣ����з��̷���������ǣ� ��
A.(x��2)2��(x��4)2��x2B.(x��2)2��(x��4)2��x2
C.x2��(x��4)2��(x��4)2D.(x��2)2��x2��(x��4)2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����ǡ�ABC�У��ֱ���AB��ACΪ���������ȱߡ�ABE�͵ȱߡ�ACD������BD��CE���Բ���BD��CE�Ĵ�С��ϵ����˵�����ɣ�
������̽����
��2����ͼ2����ABC�У���ABC=45�㣬AB=5cm��BC=3cm���ֱ���AB��ACΪ��������������ABNE��������ACMD������BD����BD�ij���
��3����ͼ3���ڣ�2���������£���ACΪֱ�DZ����߶�AC�����������ֱ�ǡ�ACD����BD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
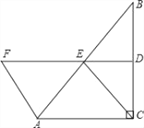
����Ŀ����ͼ���ڡ�ABC�У���ACB=90����BC�Ĵ�ֱƽ����DE��BC��D����AB��E��F��DE�ϣ�����AF=CE��
��1����֤���ı���ACEF��ƽ���ı��Σ�
��2������B����ʲô����ʱ���ı���ACEF�����Σ���ش�֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��գ���ע�����ɣ�
�������ȷ��֤������ͼ����֪AB��CD����֤����BED=��B+��D
֤������E����EF��AB������ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�У�
���1= �� ��
��AB��CD����֪��
��EF��CD���������ֱ����ͬһֱ��ƽ�У���ô����Ҳƽ�У�
���2= �� ��
�֡�BED=��1+��2
���BED=��B+��D ��������������
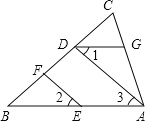
����ͼ���ڡ�ABC�У�EF��AD����1=��2����BAC=70�㣮�����AGD�Ĺ�����д������
�⣺��ΪEF��AD����֪��
���ԡ�2=��3���� ��
����Ϊ��1=��2�����ԡ�1=��3��������������
����AB�� �� ��
���ԡ�BAC+ =180�㣨 ����
����Ϊ��BAC=70�㣬���ԡ�AGD=110�㣮

ͼ�� ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӳ�ƽ���ı���ABCD�ı�DC����E��ʹCE=DC������AE����BC�ڵ�F������AC��BE��
��1����֤��BF=CF��
��2����AB=2��AD=4���ҡ�AFC=2��D����ƽ���ı���ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ڲ�����һ��P����������������ľ�����ȣ����Pһ���ǣ� ��
A. ������������ƽ���ߵĽ��� B. ������������ֱƽ���ߵĽ���
C. �������������ߵĽ��� D. �����������ߵĽ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com