
 宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,不有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们量一量把!”君哥、宾哥在楼体两侧各选A、B两点,其中CDEF表示楼体,AB=200米,CD=20米.∠A=30°,∠B=45°,(A、C、D、E四点在同一直线上)问:
宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,不有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们量一量把!”君哥、宾哥在楼体两侧各选A、B两点,其中CDEF表示楼体,AB=200米,CD=20米.∠A=30°,∠B=45°,(A、C、D、E四点在同一直线上)问:分析 (1)设楼高为x,则CF=DE=x,在Rt△ACF和Rt△DEB中分别用x表示AC、BD的值,然后根据AC+CD+BD=200,求出x的值即可;
(2)根据(1)求出楼高x,然后求出20层楼的高度,比较x和20层楼高的大小即可判断谁的观点正确.
解答 解:(1)设楼高为x米,则CF=DE=x米,
∵∠A=30°,∠B=45°,∠ACF=∠BDE=90°,
∴AC=$\sqrt{3}$x米,BD=x米,
∴$\sqrt{3}$x+x=200-20,
解得x=90($\sqrt{3}$-1)(米),
答:楼高90($\sqrt{3}$-1)米.
(2)∵x=90($\sqrt{3}$-1)≈90(1.73-1)=90×0.73=65.7米>3×20米,
∴我支持君哥的观点,这楼起码20层.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用方程思想求解,难度一般.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
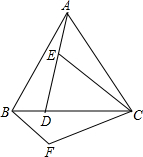 如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF.
如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
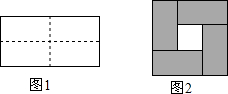 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )| A. | (m+n)2=m2+2mn+n2 | B. | (m+n)2-4mn=(m-n)2 | C. | (m+n)2-(m-n)2=4mn | D. | m2-n2=(m+n)(m-n) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
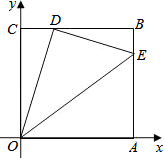 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com