练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    满足x2＝|x|的所有x的值是


    1. A.
      1
    2. B.
      -1
    3. C.
      1或-1
    4. D.
      -1或0或1
    D
    当x≥0时，x2＝x，当x＜0时，x2＝-x．解这两个方程得：x1＝0，x2＝1，x3＝-1故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：中考备考专家数学(第二版) 题型：044

    已知：抛物线y＝x2－mx＋与抛物线y＝x2＋mx－m2在平面直角坐标系xOy中的位置如图所示，其中一条与x轴交于A、B两点．

    (1)试判断哪条抛物线经过A、B两点，并说明理由；

    (2)若A、B两点到原点的距离AO、BO满足－＝，求经过A、B两点的这条抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源：非常讲解·教材全解全析　数学　九年级下　（配北师大课标） 配北师大课标 题型：013

    三金书店销售练习册所获的利润y(元)与所卖的本数x(册)之间的关系满足y＝－x2＋10000x＋24997500，则当0＜x≤4500时的最大利润为

    [　　]

    A．2500元

    B．25002500元

    C．49747500元

    D．24997500元

    查看答案和解析>>

    科目：初中数学 来源：非常讲解·教材全解全析　数学　九年级下　（配北师大课标） 配北师大课标 题型：044

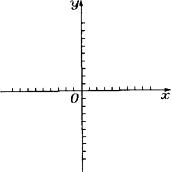
    已知：抛物线y＝－x2－(m＋3)x＋m2－12与x轴交于A(x1，0)、B(x2，0)两点，且x1＜0，x2＞0，抛物线与y轴交于点C，OB＝2OA．

    (1)求抛物线的解析式；

    (2)在x轴上，点A的左侧，求一点E，使△ECO与△CAO相似，并说明直线EC经过(1)中抛物线的顶点D；

    (3)过(2)中的点E的直线y＝x＋b与(1)中的抛物线相交于M、N两点，分别过M、N作x轴的垂线，垂足为、，点P为线段MN上一点，点P的横坐标为t，过点P作平行于y轴的直线交(1)中的所求抛物线于点Q．是否存在t值，使∶S△QMN＝35∶12，若存在，求出满足条件的t值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2006－2007柘荣二中初三数学期中试卷－北师大 题型：044

    探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”(完成下列空格)

    (1)

    当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的两边分别是x和y，由题意得方程组：

    ，消去y化简得：2x2－7x＋6＝0

    ∵△＝b2－4ac＝49－48＞0∴x1＝________，x2＝________∴满足要求的矩形B存在．

    (2)

    如果矩形A的边长为m和n，请你仿照小明的方法研究满足什么条件时，矩形B不存在？

    (3)

    如下图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y分别表示矩形B的两边长，请你结合刚才的研究，求：这个图象所研究的矩形A，B的两边长各为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （12分）今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如下表：

    周数x

    1

    2

    3

    4

    价格y（元/千克）

    2

    2.2

    2.4

    2.6

    1.（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式；

    2.（2）进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y（元/千克）从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y与周数x的变化情况满足二次函数y＝－ x2＋bx＋c. ，请求出5月份y与x的函数关系式

    3.（3）若4月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m＝x＋1.2，5月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m＝x＋2．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？

     

    查看答案和解析>>

    同步练习册答案