
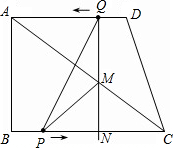
 D的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
D的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.| BC |
| AC |
| 4 |
| 5 |
| NC |
| MC |
| NC |
| MC |
| BC |
| AC |
| 4 |
| 5 |
| CN |
| cos∠NCM |
| 1+t | ||
|
| 5+5t |
| 4 |
| 3(t+1) |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3(t+1) |
| 4 |
| 3(t+1)2 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 5(t+1) |
| 4 |
9
| ||
| 2 |
| 1 |
| 2 |


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com